Question

为了了解某一地区母亲身高ｘ与女儿身高Y的相关关系，随机测得10对母女的身高如下表所示：

母亲身高ｘ（ｃｍ）	159	160	160	163	159	154	159	158	159	157
女儿身高y（ｃｍ）	158	159	160	161	161	155	162	157	162	156

试对ｘ与y进行一元线性回归分析，并预报当母亲身高为161 ｃｍ时女儿的身高为多少？

Answer 1

思路分析:为了寻找两个随机变量间的线性关系，一般先做散点图.把这10对数据画出散点图，如图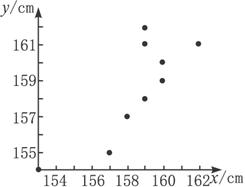3-1-1所示，

图3-1-1

其中点（159，162）表示一对母女的身高数据.由图可以看出，ｘ与y之间有近似的线性相关关系,据此用回归直线方程解决问题.

解：由以上分析先对ｘ与y作相关性检验.

（1）作统计假设：ｘ与y不具有线性相关关系.

（2）由小概率0.05与ｎ-2＝8在附表中查得r_0.05=0.632.

（3）=(159+160+…+157)=158.8,

=(158+159+…+156)=159.1，

=(159²+160²+…+157²)-10×158.8²=47.6，

-10x y=(159×158+160×159+…+157×156)-10×158.8×159.1=37.2，

∑y_i²-10y²=(158²+159²+…+156²)-10×159.1²=56.9,

所以r=≈0.71.

（4）|r|=0.71＞0.632，即|r|＞r_0.05,从而有95%的把握认为ｘ与y之间具有线性相关关系，求回归直线方程是有意义的.

    回归系数=≈0.78,=159.1-0.782×158.8≈34.92.所以y对ｘ的回归直线方程是=34.92+0.78x.因此，当母亲身高为161 ｃｍ时，女儿的身高的预报值为=34.92+0.78×160=160.5 ｃｍ.这就是说，当母亲身高为161 ｃｍ时女儿的身高大致也接近161 ｃｍ.

    方法归纳 注意此处空半格线性回归分析的步骤方法为：①首先作出统计假设;②求出线性相关系数;③由相关系数确定回归直线方程是否有意义;④写出线性回归方程，解决有关问题.