题目内容
函数 的定义域为A,若2∉A,则a的取值范围是
的定义域为A,若2∉A,则a的取值范围是
- A.1<a<3
- B.1≤a≤3
- C.a≥3或a≤1
- D.a>3或a<1
A
分析:由二次根式的被开方数必须非负,得函数的定义域A={x|x2-2ax+a2-1≥0},再根据2∉A,得当x=2时,x2-2ax+a2-1<0成立,由此建立关于a的不等式,解之即得实数a的取值范围.
解答:根据题意,得函数的定义域A={x|x2-2ax+a2-1≥0}
∵2∉A,
∴当x=2时,x2-2ax+a2-1<0成立
即4-4a+a2-1<0,解之得1<a<3
故选:A
点评:本题给出实数2不在函数的定义域内,求参数a的取值范围,着重考查了函数定义域的求法和一元二次不等式的解法等知识,属于基础题.
分析:由二次根式的被开方数必须非负,得函数的定义域A={x|x2-2ax+a2-1≥0},再根据2∉A,得当x=2时,x2-2ax+a2-1<0成立,由此建立关于a的不等式,解之即得实数a的取值范围.
解答:根据题意,得函数的定义域A={x|x2-2ax+a2-1≥0}
∵2∉A,
∴当x=2时,x2-2ax+a2-1<0成立
即4-4a+a2-1<0,解之得1<a<3
故选:A
点评:本题给出实数2不在函数的定义域内,求参数a的取值范围,着重考查了函数定义域的求法和一元二次不等式的解法等知识,属于基础题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 的定义域为A,若
的定义域为A,若 且
且 时总有
时总有 ,则称
,则称 是单函数.下列命题:
是单函数.下列命题: 是单函数;
是单函数; 则
则 ;
; B为单函数,则对于任意b
B为单函数,则对于任意b B,它至多有一个原象;
B,它至多有一个原象; 的定义域为A,若
的定义域为A,若 且
且 时总有
时总有 ,则称
,则称 )是单函数.下列命题
)是单函数.下列命题 (x
(x R)是单函数
R)是单函数 (x
(x ,则
,则 ;
; 的定义域为A,若
的定义域为A,若 时总有
时总有 为单函数.例如,函数
为单函数.例如,函数 )是单函数.下列命题:
)是单函数.下列命题: (x
(x R)是单函数;
R)是单函数;
 B为单函数,则对于任意b
B为单函数,则对于任意b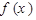 的定义域为A,若
的定义域为A,若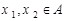 且
且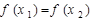 时总有
时总有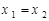 ,则称
,则称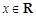 )是单函数.下列命题:
)是单函数.下列命题: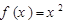 (x
(x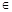 R)是单函数;
R)是单函数;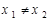 ,则
,则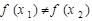 ;
;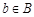 ,它至多有一个原象;
,它至多有一个原象;