题目内容
已知椭圆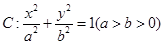 过点
过点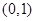 且离心率为
且离心率为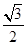 .
.
(1)求椭圆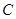 的方程;
的方程;
(2)若斜率为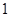 的直线
的直线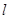 交
交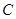 于
于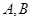 两点,且
两点,且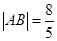 ,求直线
,求直线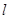 的方程.
的方程.
(1) ;(2)直线
;(2)直线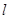 的方程为
的方程为 .
.
解析试题分析:(1)先根据椭圆过点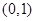 确定
确定 ,进而根据离心率及椭圆中
,进而根据离心率及椭圆中 的关系式得到
的关系式得到 ,进而求解出
,进而求解出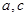 即可确定椭圆
即可确定椭圆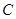 的方程;(2)设
的方程;(2)设 及直线
及直线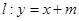 ,进而联立直线与椭圆的方程得到
,进而联立直线与椭圆的方程得到 ,消
,消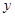 得到
得到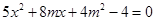 ,进而根据二次方程根与系数的关系可得
,进而根据二次方程根与系数的关系可得 ,
, ,进而代入弦长公式
,进而代入弦长公式 ,从中即可求解出
,从中即可求解出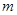 的值,进而可确定直线
的值,进而可确定直线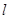 的方程.
的方程.
(1)由题知 ,又因为
,又因为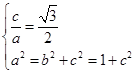 ,从中求解得到
,从中求解得到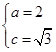
则椭圆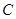 的方程为
的方程为
(2)设 ,直线
,直线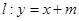
由 ,消去
,消去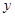 得到
得到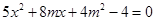
则 ,
,
则
解得 ,又直线
,又直线 与
与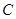 有两个交点
有两个交点
故直线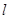 的方程为
的方程为 .
.
考点:1.椭圆的标准方程及其几何性质;2.直线与椭圆的位置关系;3.二次方程根与系数的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
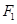 ,
,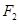 分别是椭圆
分别是椭圆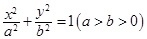 的左右焦点,M是C上一点且
的左右焦点,M是C上一点且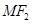 与x轴垂直,直线
与x轴垂直,直线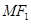 与C的另一个交点为N.
与C的另一个交点为N.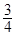 ,求C的离心率;
,求C的离心率;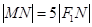 ,求a,b.
,求a,b.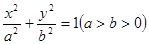 的离心率为
的离心率为 ,点
,点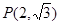 在椭圆上.
在椭圆上. 的动直线与椭圆交于M,N两点,连接AN、BM相交于G点,试求点G的横坐标的值.
的动直线与椭圆交于M,N两点,连接AN、BM相交于G点,试求点G的横坐标的值. 的方程为
的方程为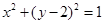 ,定直线
,定直线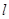 的方程为
的方程为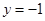 .动圆
.动圆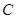 与圆
与圆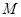 的方程;
的方程;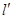 与轨迹
与轨迹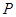 , 过点
, 过点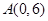 ,并交轨迹
,并交轨迹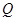 ,求直线
,求直线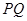 的方程及
的方程及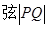 的长.
的长.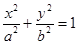 上的点M与椭圆右焦点
上的点M与椭圆右焦点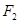 的连线
的连线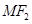 与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.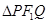 的面积是20,求此时椭圆的方程.
的面积是20,求此时椭圆的方程.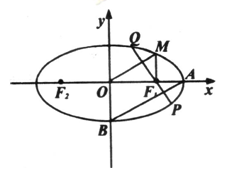
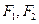 分别是椭圆
分别是椭圆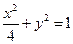 的 左,右焦点。
的 左,右焦点。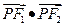 的 最大值和最小值。
的 最大值和最小值。 的左焦点为F1(-1,0),且点P(0,1)在C1上。
的左焦点为F1(-1,0),且点P(0,1)在C1上。 相切,求直线l的方程.
相切,求直线l的方程.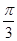 ,且△PF1F2的面积为2
,且△PF1F2的面积为2 ,双曲线的离心率为2,求该双曲线的标准方程.
,双曲线的离心率为2,求该双曲线的标准方程.