Question

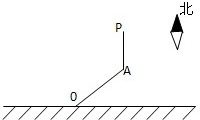在东西方向直线延伸的湖岸上有一港口O，一艘机艇以40km/h的速度从O港出发，先沿东偏北的某个方向直线前进到达A处，然后改向正北方向航行，总共航行30分钟因机器出现故障而停在湖里的P处，由于营救人员不知该机艇的最初航向及何时改变的航向，故无法确定机艇停泊的准确位置，试划定一个最佳的弓形营救区域（用图形表示），并说明你的理由．

Answer 1

分析：以O为原点，湖岸线为x轴建立直角坐标系，设OA的倾斜角为θ，点P的坐标为（x，y），|OA|=m，|AP|=n，则有

x=mcosθ y=n+msinθ m+n=20

(0＜θ＜

π

2

)，由此能够导出营救区域为直线x+y=20与圆x²+y²=400围城的弓形区域．

解答：解：以O为原点，湖岸线为x轴建立直角坐标系，设OA的倾斜角为θ，点P的坐标为（x，y），
|OA|=m，|AP|=n，则有　（3分）

x=mcosθ y=n+msinθ m+n=20

(0＜θ＜

π

2

)（7分）
由此得

x2+y2=m2+n2+2mnsinθ x+y=m(sinθ+cosθ)+n

（9分）
即

x2+y2＜m2+n2+2mn=(m+n)2=400 x+y= 2 msin(θ+ π 4 )+n＞ 2 m• 2 2 +n=20

（12分）
故营救区域为直线x+y=20与圆x²+y²=400围城的弓形区域．（14分）

点评：本题考查圆的性质和应用，解题时要认真审题，仔细解答，注意合理地选用公式．