题目内容
设函数
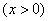 .
.
(1)求函数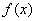 的最小值;
的最小值;
(2)设
 ,讨论函数
,讨论函数 的单调性;
的单调性;
(3)斜率为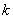 的直线与
的直线与 交于
交于 ,
,
 两点,求证:
两点,求证: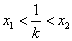 .
.
(1)解:f'(x)=lnx+1(x>0),令f'(x)=0,得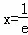 .
.
∵当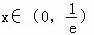 时,f'(x)<0;当
时,f'(x)<0;当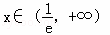 时,
时,
f'(x)>0,
∴当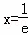 时,
时,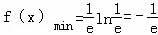 .----------------- 4分
.----------------- 4分
(2)F(x)=ax2+lnx+1(x>0), .
.
①当a≥0时,恒有F'(x)>0,F(x)在(0,+∞)上是增函数;
②当a<0时,
令F'(x)>0,得2ax2+1>0,解得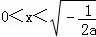 ;
;
令F'(x)<0,得2ax2+1<0,解得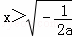 .
.
综上,当a≥0时,F(x)在(0,+∞)上是增函数;
当a<0时,F(x)在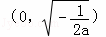 上单调递增,在
上单调递增,在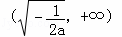 上单调递减.------------------------------------8分
上单调递减.------------------------------------8分
(3)证: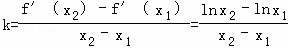 .
.
要证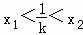 ,即证
,即证 ,等价于证
,等价于证 ,令
,令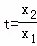 ,
,
则只要证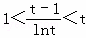 ,由t>1知lnt>0,
,由t>1知lnt>0,
故等价于证lnt<t﹣1<tlnt(t>1)(*).
①设g(t)=t﹣1﹣lnt(t≥1),则 ,
,
故g(t)在[1,+∞)上是增函数,
∴当t>1时,g(t)=t﹣1﹣lnt>g(1)=0,即t﹣1>lnt(t>1).
②设h(t)=tlnt﹣(t﹣1)(t≥1),则h'(t)=lnt≥0(t≥1),故h(t)在[1,+∞)上是增函数,
∴当t>1时,h(t)=tlnt﹣(t﹣1)>h(1)=0,即t﹣1<tlnt(t>1).
由①②知(*)成立,得证.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
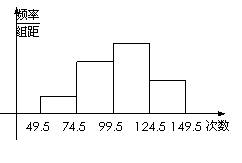 (Ⅰ)求第四小组的频率和参加这次测试的学生人数;
(Ⅰ)求第四小组的频率和参加这次测试的学生人数; |=|
|=| |=2,(
|=2,( ,集合
,集合 ,集合
,集合 ,则集合
,则集合 的面积是 ( )
的面积是 ( ) B.
B. C.
C. D.
D.
 ,
,
 ,求
,求 ;
; 的三边
的三边 满足
满足 ,且边
,且边 所对应的角为
所对应的角为 ,若关于
,若关于 有且仅有一个实数根,求
有且仅有一个实数根,求 的值.
的值. 若
若 ,则
,则 是
是 的充分而不必要条件;
的充分而不必要条件; 函数
函数 的定义域是
的定义域是 ,则( )
,则( ) 或
或 ”为假 B.“
”为假 B.“ 的焦点
的焦点 、
、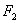 ,点
,点 为其上的动点,当∠
为其上的动点,当∠ ,且
,且 成等比数列,则
成等比数列,则 有
有 B、最小值
B、最小值 C、最大值
C、最大值