题目内容
如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥平面ACE,
(1)求证:AE⊥BC;
(2)如果点N为线段AB的中点,求证:MN∥平面ADE。
(1)求证:AE⊥BC;
(2)如果点N为线段AB的中点,求证:MN∥平面ADE。

证明:(1)因为BM⊥平面ACE,AE 平面ACE,
平面ACE,
所以BM⊥AE,
因为AE⊥BE,且BE∩BM=B,BE、BM 平面EBC,
平面EBC,
所以AE⊥平面EBC,
因为BC 平面EBC,
平面EBC,
所以AE⊥BC。
(2)取DE中点H,连接MH、AH,
因为BM⊥平面ACE,EC 平面ACE,
平面ACE,
所以BM⊥EC,因为BE=BC,
所以M为CE的中点,
所以MH为△EDC的中位线,所以MH
 DC,
DC,
因为四边形ABCD为平行四边形,所以DC∥AB,故MH
 AB,
AB,
因为N为AB的中点,所以MH AN,
AN,
所以四边形ANMH为平行四边形,所以MN∥AH,
因为MN 平面ADE,AH
平面ADE,AH 平面ADE,
平面ADE,
所以MN∥平面ADE。
 平面ACE,
平面ACE,所以BM⊥AE,
因为AE⊥BE,且BE∩BM=B,BE、BM
 平面EBC,
平面EBC,所以AE⊥平面EBC,
因为BC
 平面EBC,
平面EBC,所以AE⊥BC。
(2)取DE中点H,连接MH、AH,
因为BM⊥平面ACE,EC
 平面ACE,
平面ACE,所以BM⊥EC,因为BE=BC,
所以M为CE的中点,
所以MH为△EDC的中位线,所以MH

 DC,
DC,因为四边形ABCD为平行四边形,所以DC∥AB,故MH

 AB,
AB,因为N为AB的中点,所以MH
 AN,
AN,所以四边形ANMH为平行四边形,所以MN∥AH,
因为MN
 平面ADE,AH
平面ADE,AH 平面ADE,
平面ADE,所以MN∥平面ADE。

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
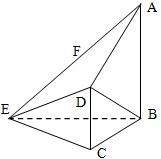 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°,F为AE中点.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°,F为AE中点. 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.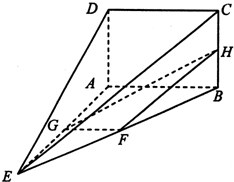 (2013•贵阳二模)如图,在四棱锥E-ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点
(2013•贵阳二模)如图,在四棱锥E-ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点 (2012•淮南二模)如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥面ACE.
(2012•淮南二模)如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥面ACE. 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,