题目内容
数列1,-3,5,-7,9,……的一个通项公式为( )
A. | B. |
C. | D. |
B
解析试题分析:本题分两部分看,一看数的变化,都是正奇数,表示为 2n-1, 二看符号,分别在偶数位置出现负号,表示为 ,和在一起,整理,即得
,和在一起,整理,即得 .故选B.
.故选B.
考点:归纳法求通项公式.

练习册系列答案
相关题目
已知数列{an}满足an=n·pn(n∈N+,0< p<l),下面说法正确的是( )
①当p=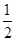 时,数列{an}为递减数列;②当
时,数列{an}为递减数列;②当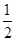 <p<l时,数列{an}不一定有最大项;
<p<l时,数列{an}不一定有最大项;
③当0<p<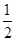 时,数列{an}为递减数列;
时,数列{an}为递减数列;
④当 为正整数时,数列{an}必有两项相等的最大项
为正整数时,数列{an}必有两项相等的最大项
| A.①② | B.③④ | C.②④ | D.②③ |
在等差数列{an}中,其前n项和是 ,若
,若 ,则在
,则在 中最大的是( )
中最大的是( )
A. | B. | C. | D. |
数列 :
: 、3、
、3、 、9、的一个通项公式是( )
、9、的一个通项公式是( )
A.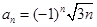 ( (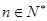 ) ) | B. ( (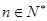 ) ) |
C. ( (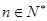 ) ) | D. ( (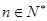 ) ) |
现有数列 满足:
满足: ,且对任意的m,n∈N*都有:
,且对任意的m,n∈N*都有: ,则
,则 ( )
( )
A. | B. | C. | D. |
已知正项数列{an}满足a1=1,(n+2)an+12-(n+1) +anan+1=0,则它的通项公式为( ).
+anan+1=0,则它的通项公式为( ).
A.an= | B.an= |
C.an= | D.an=n |
 中,角
中,角 、
、 、
、 成等差数列,且
成等差数列,且 .
.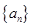 满足
满足 ,前
,前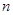 项为和
项为和 ,若
,若 ,求
,求 ﹜满足:
﹜满足: .(Ⅰ)求数列﹛
.(Ⅰ)求数列﹛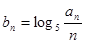 ,求
,求

