题目内容
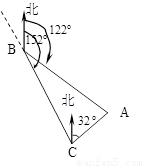
 如图,货轮在海上以40km/h的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为1400的方向航行,为了确定船的位置,船在B点观测灯塔A的方位角为1100,航行
如图,货轮在海上以40km/h的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为1400的方向航行,为了确定船的位置,船在B点观测灯塔A的方位角为1100,航行| 1 |
| 2 |
分析:在△ABC中利用三角形内角和求得∠BCA和∠BAC,则BC可求得,最后利用正弦定理求得AC.
解答:解:在△ABC中,BC=40×0.5=20km,∠ABC=140°-110°=30°,
∠ACB=65°+(180°-140°)=105°,
∴∠BAC=45°,BC=40×
=20 km
根据正弦定理可得,AC=
=
=10
.
货轮到达C点时与灯塔的距离是约10
km.
故选:C.

∠ACB=65°+(180°-140°)=105°,
∴∠BAC=45°,BC=40×
| 1 |
| 2 |
根据正弦定理可得,AC=
| BC•sin∠ABC |
| sin∠BAC |
20×
| ||||
|
| 2 |
货轮到达C点时与灯塔的距离是约10
| 2 |
故选:C.
点评:本题主要考查了解三角形的实际应用.解题的关键是建立三角函数的数学模型,运用三角函数的基础知识来解决实际问题.

练习册系列答案
相关题目
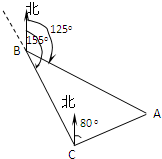 如图,货轮在海上以50浬/时的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为155°的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为125°.半小时后,货轮到达C点处,观测到灯塔A的方位角为80°.求此时货轮与灯塔之间的距离(得数保留最简根号).
如图,货轮在海上以50浬/时的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为155°的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为125°.半小时后,货轮到达C点处,观测到灯塔A的方位角为80°.求此时货轮与灯塔之间的距离(得数保留最简根号). 如图,货轮在海上以35n mile/h的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为152°的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为122°.半小时后,货轮到达C点处,观测到灯塔A的方位角为32°.求此时货轮与灯塔之间的距离.
如图,货轮在海上以35n mile/h的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为152°的方向航行.为了确定船位,在B点处观测到灯塔A的方位角为122°.半小时后,货轮到达C点处,观测到灯塔A的方位角为32°.求此时货轮与灯塔之间的距离.