题目内容
设a是实数,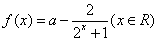 。
。
(1)试证明对于任意的a,f(x)为增函数;
(2)试确定a的值,使f(x)为奇函数。
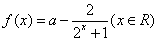 。
。(1)试证明对于任意的a,f(x)为增函数;
(2)试确定a的值,使f(x)为奇函数。
解:(1)设 ,且
,且 ,
,
则 ,
,
由于 在R上是增函数,且
在R上是增函数,且 ,
,
所以, ,
,
即 ,
,
又 ,得
,得 ,
,
所以, ,
,
即 ,因此与a的取值无关,
,因此与a的取值无关,
故对于任意的实数a,f(x)为增函数。
(2)若f(x)为奇函数,又因为f(x)的定义域为R,
故有f(0)=0,即 ,即a=1。
,即a=1。
 ,且
,且 ,
,则
 ,
,由于
 在R上是增函数,且
在R上是增函数,且 ,
,所以,
 ,
,即
 ,
,又
 ,得
,得 ,
,所以,
 ,
,即
 ,因此与a的取值无关,
,因此与a的取值无关,故对于任意的实数a,f(x)为增函数。
(2)若f(x)为奇函数,又因为f(x)的定义域为R,
故有f(0)=0,即
 ,即a=1。
,即a=1。 
练习册系列答案
相关题目
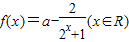 ,
,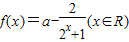 .
.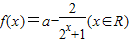 .
.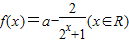 .
.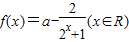 .
.