题目内容
已知a>0,函数f(x)=lnx-ax2,x>0.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若存在均属于区间[1,3]的α,β,且β-α≥1,使f(α)=f(β),证明 .
.
(I)解: ,
,
令f′(x)=0,解得x=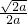 ,
,
当x变化时,f'(x),f(x)的变化情况如下表:
所以,f(x)的单调递增区间是 的单调递减区间是
的单调递减区间是 .
.
(II)证明:由f(α)=f(β)及(I)的结论知 ,
,
从而f(x)在[α,β]上的最小值为f(a).
又由β-α≥1,α,β∈[1,3],
知1≤α≤2≤β≤3.
故 ,
,
即 ,
,
从而 .
.
分析:(I)由 ,令f′(x)=0,解得x=
,令f′(x)=0,解得x=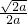 ,列表讨论能求出f(x)的单调递增区间和单调递减区间.
,列表讨论能求出f(x)的单调递增区间和单调递减区间.
(II)由f(α)=f(β)及(I)的结论知 ,从而f(x)在[α,β]上的最小值为f(a).由β-α≥1,α,β∈[1,3],知1≤α≤2≤β≤3.由此能够证明
,从而f(x)在[α,β]上的最小值为f(a).由β-α≥1,α,β∈[1,3],知1≤α≤2≤β≤3.由此能够证明 .
.
点评:本题考查函数单调区间的求法和利用导数求闭区间上函数最值的应用,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.
 ,
,令f′(x)=0,解得x=
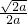 ,
,当x变化时,f'(x),f(x)的变化情况如下表:
| x |  | 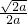 |  |
| f'(x) | + | 0 | - |
| f(x) | ↑ | 极大值 | ↓ |
 的单调递减区间是
的单调递减区间是 .
.(II)证明:由f(α)=f(β)及(I)的结论知
 ,
,从而f(x)在[α,β]上的最小值为f(a).
又由β-α≥1,α,β∈[1,3],
知1≤α≤2≤β≤3.
故
 ,
,即
 ,
,从而
 .
.分析:(I)由
 ,令f′(x)=0,解得x=
,令f′(x)=0,解得x=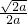 ,列表讨论能求出f(x)的单调递增区间和单调递减区间.
,列表讨论能求出f(x)的单调递增区间和单调递减区间.(II)由f(α)=f(β)及(I)的结论知
 ,从而f(x)在[α,β]上的最小值为f(a).由β-α≥1,α,β∈[1,3],知1≤α≤2≤β≤3.由此能够证明
,从而f(x)在[α,β]上的最小值为f(a).由β-α≥1,α,β∈[1,3],知1≤α≤2≤β≤3.由此能够证明 .
.点评:本题考查函数单调区间的求法和利用导数求闭区间上函数最值的应用,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知a>0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
| A、?x∈R,f(x)≤f(x0) | B、?x∈R,f(x)≥f(x0) | C、?x∈R,f(x)≤f(x0) | D、?x∈R,f(x)≥f(x0) |