题目内容
已知函数f(x)=2sin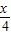 •cos
•cos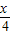 +
+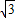 cos
cos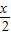 .
.(1)求函数f(x)的最小正周期及最值;
(2)令g(x)=f
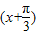 ,判断函数g(x)的奇偶性,并说明理由.
,判断函数g(x)的奇偶性,并说明理由.
【答案】分析:利用二倍角公式、两角和的正弦函数化简函数f(x)=2sin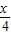 •cos
•cos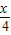 +
+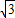 cos
cos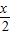 ,为y=2sin
,为y=2sin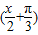 ,
,
(1)直接利用周期公式求出周期,求出最值.
(2)求出g(x)=f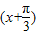 的表达式,g(x)=2cos
的表达式,g(x)=2cos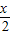 .然后判断出奇偶性即可.
.然后判断出奇偶性即可.
解答:解:(1)∵f(x)=sin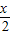 +
+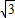 cos
cos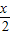 =2sin
=2sin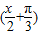 ,
,
∴f(x)的最小正周期T=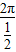 =4π.
=4π.
当sin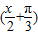 =-1时,f(x)取得最小值-2;
=-1时,f(x)取得最小值-2;
当sin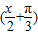 =1时,f(x)取得最大值2.
=1时,f(x)取得最大值2.
(2)g(x)是偶函数.理由如下:
由(1)知f(x)=2sin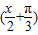 ,
,
又g(x)=f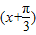 ,
,
∴g(x)=2sin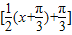
=2sin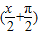 =2cos
=2cos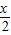 .
.
∵g(-x)=2cos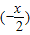 =2cos
=2cos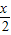 =g(x),
=g(x),
∴函数g(x)是偶函数.
点评:本题是基础题,考查三角函数的化简与求值,考查三角函数的基本性质,常考题型.
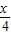 •cos
•cos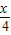 +
+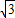 cos
cos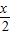 ,为y=2sin
,为y=2sin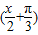 ,
,(1)直接利用周期公式求出周期,求出最值.
(2)求出g(x)=f
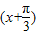 的表达式,g(x)=2cos
的表达式,g(x)=2cos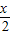 .然后判断出奇偶性即可.
.然后判断出奇偶性即可.解答:解:(1)∵f(x)=sin
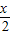 +
+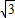 cos
cos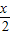 =2sin
=2sin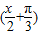 ,
,∴f(x)的最小正周期T=
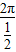 =4π.
=4π.当sin
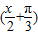 =-1时,f(x)取得最小值-2;
=-1时,f(x)取得最小值-2;当sin
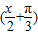 =1时,f(x)取得最大值2.
=1时,f(x)取得最大值2.(2)g(x)是偶函数.理由如下:
由(1)知f(x)=2sin
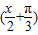 ,
,又g(x)=f
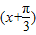 ,
,∴g(x)=2sin
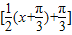
=2sin
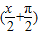 =2cos
=2cos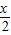 .
.∵g(-x)=2cos
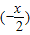 =2cos
=2cos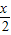 =g(x),
=g(x),∴函数g(x)是偶函数.
点评:本题是基础题,考查三角函数的化简与求值,考查三角函数的基本性质,常考题型.

练习册系列答案
相关题目