题目内容
（满分12分）已知动圆C过定点
，且与圆A：
相内切。
（1）求动圆的圆心C的轨迹方程
（2）若P是动圆圆心轨迹上的一点，
为圆A的圆心且
，求
的面积
解：（1）设切点为N，动圆与圆O内切，则F2，M，N三点共线，且|MF1|=|MN|
即M到定点F1，F2的距离之和为定值10>|F1F2|=6
故M的轨迹是以F1，F2为焦点的椭圆
易知c=3，a=5，b=4
M的轨迹方程是
5分
（2）设|PF1|=r1，|PF2|=r2，
则
（1）
又在
中，由勾股定理得
（2）
（1）—（2）得
7分
练习册系列答案
相关题目
过点
，且与圆
相内切.
（其中
与（1）中所求轨迹交于不同两点
，D，与双曲线
交于不同两点
，问是否存在直线
，使得向量
，若存在，指出这样的直线有多少条？若不存在，请说明理由．
过点
，且与
圆
相内切．
（其中
与（1）中所求轨迹交于不同两点
，D
，与双曲线
交于不同两点
，问是否存在直线
，使得向量
，若存在，指出这样的直线有多少条？若不存在，请说明理由．
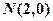并且与圆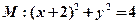
相外切，动圆圆心P的轨迹为W，过点N的直线
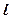与轨迹W交于A、B两点。
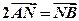，求直线
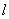的方程；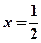
上是否存在一点Q，使得
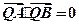，并说明理由。
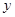轴的距离大1个单位长度。
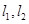，分别交曲线C于点A、B和M、N，设线段AB、MN的中点分别为P、Q，求证：直线PQ恒过一个定点。
过点
，且与圆
相内切．
（其中
与（1）中所求轨迹交于不同两点
，D，与双曲线
交于不同两点
，问是否存在直线
，使得向量
，若存在，指出这样的直线有多少条？若不存在，请说明理由．