题目内容
已知等比数列{an}满足a1•a4•a7=1,a2•a5•a8=8,则a3•a6•a9的值为
- A.8
- B.16
- C.32
- D.64
D
分析:先根据等比数列性质求出a4,a5,从而求出a6,最后可求出a3•a6•a9=a63的值.
解答:∵等比数列{an}满足a1•a4•a7=1,a2•a5•a8=8
∴a43=1即a4=1,a53=8即a5=2
∴公比q=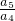 =2,则a6=4
=2,则a6=4
a3•a6•a9=a63=43=64
故选D.
点评:本题主要考查了等比数列的性质,以及等比数列的通项公式,解题的关键是利用性质化简变形,属于基础题.
分析:先根据等比数列性质求出a4,a5,从而求出a6,最后可求出a3•a6•a9=a63的值.
解答:∵等比数列{an}满足a1•a4•a7=1,a2•a5•a8=8
∴a43=1即a4=1,a53=8即a5=2
∴公比q=
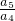 =2,则a6=4
=2,则a6=4a3•a6•a9=a63=43=64
故选D.
点评:本题主要考查了等比数列的性质,以及等比数列的通项公式,解题的关键是利用性质化简变形,属于基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目