题目内容
函数 的一个零点为
的一个零点为 ,且
,且 ,对于下列结论:
,对于下列结论:
① ;②
;② ;③
;③
④f(x)的单调减区间是 ;
;
⑤f(x)的单调增区间是 .
.
其中正确的结论是________.(填写所有正确的结论编号)
①②⑤
分析:由题意可得f(x)= sin(
sin( x+φ),由f(
x+φ),由f( )=0,
)=0, ,可确定φ,从而对①②③④⑤逐个判断即可.
,可确定φ,从而对①②③④⑤逐个判断即可.
解答:由题意可得:f(x)= sin(
sin( x+φ),
x+φ),
∵f( )=0,
)=0,
∴sin( +φ)=0,
+φ)=0,
∴φ=kπ- (k∈Z).不妨取φ=-
(k∈Z).不妨取φ=- 或φ=
或φ= ;
;
又 ,即sin(
,即sin( ×
× +φ)<sin(
+φ)<sin( ×
× +φ)<0,
+φ)<0,
∴φ= .
.
∴f(x)= sin(
sin( x+
x+ ),
),
对于①,f( )=
)= sin(
sin( ×
× +
+ )=
)= sin3π=0,故①正确;
sin3π=0,故①正确;
对于②f( )=
)= sin(
sin( ×
× +
+ )=
)= sin
sin =-
=- .
.
∴f(x)= sin(
sin( x+
x+ )≥-
)≥- =f(
=f( ),即②正确;
),即②正确;
对于③,∵f( )=
)= sin(
sin( ×
× +
+ )=
)= sin
sin =-
=- sin
sin .
.
f(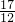 )=
)= sin(
sin( ×
×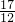 +
+ )=
)= sin
sin =-
=- sin
sin ≠f(
≠f( ).故③错误;
).故③错误;
对于④,由2kπ+ ≤
≤ x+
x+ ≤2kπ+
≤2kπ+ ,(k∈Z)得其单调递减区间为:x∈[4k-
,(k∈Z)得其单调递减区间为:x∈[4k- ,4k+
,4k+ ].故④错误.
].故④错误.
对于⑤,由2kπ+ ≤
≤ x+
x+ ≤2kπ+
≤2kπ+ ,(k∈Z)得其单调递增区间为:x∈[4k+
,(k∈Z)得其单调递增区间为:x∈[4k+ ,4k+
,4k+ ].故⑤正确.
].故⑤正确.
故答案为:①②⑤.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,着重考查辅助角公式的应用及正弦函数的性质,考查学生综合分析与转化运用知识解决问题的能力,属于难题.
分析:由题意可得f(x)=
 sin(
sin( x+φ),由f(
x+φ),由f( )=0,
)=0, ,可确定φ,从而对①②③④⑤逐个判断即可.
,可确定φ,从而对①②③④⑤逐个判断即可.解答:由题意可得:f(x)=
 sin(
sin( x+φ),
x+φ),∵f(
 )=0,
)=0,∴sin(
 +φ)=0,
+φ)=0,∴φ=kπ-
 (k∈Z).不妨取φ=-
(k∈Z).不妨取φ=- 或φ=
或φ= ;
;又
 ,即sin(
,即sin( ×
× +φ)<sin(
+φ)<sin( ×
× +φ)<0,
+φ)<0,∴φ=
 .
.∴f(x)=
 sin(
sin( x+
x+ ),
),对于①,f(
 )=
)= sin(
sin( ×
× +
+ )=
)= sin3π=0,故①正确;
sin3π=0,故①正确;对于②f(
 )=
)= sin(
sin( ×
× +
+ )=
)= sin
sin =-
=- .
.∴f(x)=
 sin(
sin( x+
x+ )≥-
)≥- =f(
=f( ),即②正确;
),即②正确;对于③,∵f(
 )=
)= sin(
sin( ×
× +
+ )=
)= sin
sin =-
=- sin
sin .
.f(
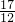 )=
)= sin(
sin( ×
×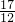 +
+ )=
)= sin
sin =-
=- sin
sin ≠f(
≠f( ).故③错误;
).故③错误;对于④,由2kπ+
 ≤
≤ x+
x+ ≤2kπ+
≤2kπ+ ,(k∈Z)得其单调递减区间为:x∈[4k-
,(k∈Z)得其单调递减区间为:x∈[4k- ,4k+
,4k+ ].故④错误.
].故④错误.对于⑤,由2kπ+
 ≤
≤ x+
x+ ≤2kπ+
≤2kπ+ ,(k∈Z)得其单调递增区间为:x∈[4k+
,(k∈Z)得其单调递增区间为:x∈[4k+ ,4k+
,4k+ ].故⑤正确.
].故⑤正确.故答案为:①②⑤.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,着重考查辅助角公式的应用及正弦函数的性质,考查学生综合分析与转化运用知识解决问题的能力,属于难题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 的一个零点为
的一个零点为 ,且
,且 ,对于下列结论:
,对于下列结论: ;②
;② ;③
;③
 ;
; .
. 的一个零点为
的一个零点为 ,且
,且 ,对于下列结论:
,对于下列结论: ;②
;② ;③
;③
 ;
; .
. 的一个零点为
的一个零点为 ,且
,且 ,对于下列结论:
,对于下列结论: ;②
;② ;③
;③
 ;
; .
.