题目内容
已知函数f(x)的定义域为(0,+∞),且对任意的正实数x,y都有f(xy)=f(x)+f(y),且当x>1时,f(x)>0,f(4)=1,
(1)求证:f(1)=0;
(2)求f( );
);
(3)解不等式f(x)+f(x-3)≤1.
解:(1)证明:令x=4,y=1,则f(4)=f(4×1)=f(4)+f(1).
∴f(1)=0.
(2)f(16)=f(4×4)=f(4)+f(4)=2,f(1)=f( ×16)=f(
×16)=f( )+f(16)=0,
)+f(16)=0,
故f( )=-2.
)=-2.
(3)设x1,x2>0且x1>x2,于是f( )>0,
)>0,
∴f(x1)=f( ×x2)=f(
×x2)=f( )+f(x2)>f(x2).
)+f(x2)>f(x2).
∴f(x)为x∈(0,+∞)上的增函数.
又∵f(x)+f(x-3)=f[x(x-3)]≤1=f(4),
∴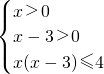 ?3<x≤4.
?3<x≤4.
∴原不等式的解集为{x|3<x≤4}.
分析:(1)根据对任意的正实数x,y都有f(xy)=f(x)+f(y),令x=4,y=1,即可求出f(1)的值;
(2)令x=4,y=4,代入求得f(16),而f(1)=f( ×16)=f(
×16)=f( )+f(16)=0,即可求得f(
)+f(16)=0,即可求得f( )的值;
)的值;
(3)根据当x>1时,f(x)>0,判断函数的单调性,把f(x)+f(x-3)≤1化为f[x(x-3)]≤1=f(4),根据单调性,去掉对应法则f,解不等式.
点评:此题是个中档题题,考查抽象函数及其应用,以及利用函数单调性的定义判断函数的单调性,并根据函数的单调性解函数值不等式,体现了转化的思想,在转化过程中一定注意函数的定义域.解决抽象函数的问题一般应用赋值法.
∴f(1)=0.
(2)f(16)=f(4×4)=f(4)+f(4)=2,f(1)=f(
 ×16)=f(
×16)=f( )+f(16)=0,
)+f(16)=0,故f(
 )=-2.
)=-2.(3)设x1,x2>0且x1>x2,于是f(
 )>0,
)>0,∴f(x1)=f(
 ×x2)=f(
×x2)=f( )+f(x2)>f(x2).
)+f(x2)>f(x2).∴f(x)为x∈(0,+∞)上的增函数.
又∵f(x)+f(x-3)=f[x(x-3)]≤1=f(4),
∴
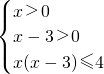 ?3<x≤4.
?3<x≤4.∴原不等式的解集为{x|3<x≤4}.
分析:(1)根据对任意的正实数x,y都有f(xy)=f(x)+f(y),令x=4,y=1,即可求出f(1)的值;
(2)令x=4,y=4,代入求得f(16),而f(1)=f(
 ×16)=f(
×16)=f( )+f(16)=0,即可求得f(
)+f(16)=0,即可求得f( )的值;
)的值;(3)根据当x>1时,f(x)>0,判断函数的单调性,把f(x)+f(x-3)≤1化为f[x(x-3)]≤1=f(4),根据单调性,去掉对应法则f,解不等式.
点评:此题是个中档题题,考查抽象函数及其应用,以及利用函数单调性的定义判断函数的单调性,并根据函数的单调性解函数值不等式,体现了转化的思想,在转化过程中一定注意函数的定义域.解决抽象函数的问题一般应用赋值法.

练习册系列答案
相关题目
