题目内容
设an是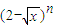 的展开式中x项的系数(n=2,3,4,…),则极限
的展开式中x项的系数(n=2,3,4,…),则极限 = .
= .
【答案】分析:根据已知条件求出 an=n(n-1)2n-3,用裂项法求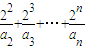 的和,再用数列极限的运算法则求得
的和,再用数列极限的运算法则求得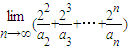 的运算结果.
的运算结果.
解答:解: 的展开式通项公式Tr+1=
的展开式通项公式Tr+1=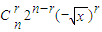 ,令r=2 可得
,令r=2 可得
T3=Cn22n-2x,∴an =Cn22n-2=n(n-1)2n-3.
∴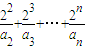 =
=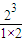 +
+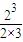 +…+
+…+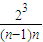
=23 (1- +
+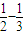 +…
+…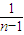 -
-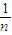 )=8×(1-
)=8×(1- ).
).
∴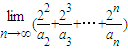 =
=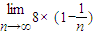 =8,
=8,
故答案为:8.
点评:本题考查求展开式中某项的系数,用裂项法进行数列求和,数列极限的运算法则的应用,属于难题.
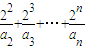 的和,再用数列极限的运算法则求得
的和,再用数列极限的运算法则求得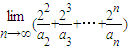 的运算结果.
的运算结果.解答:解:
 的展开式通项公式Tr+1=
的展开式通项公式Tr+1=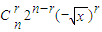 ,令r=2 可得
,令r=2 可得T3=Cn22n-2x,∴an =Cn22n-2=n(n-1)2n-3.
∴
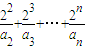 =
=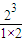 +
+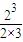 +…+
+…+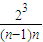
=23 (1-
 +
+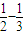 +…
+…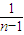 -
-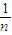 )=8×(1-
)=8×(1- ).
).∴
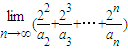 =
=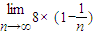 =8,
=8,故答案为:8.
点评:本题考查求展开式中某项的系数,用裂项法进行数列求和,数列极限的运算法则的应用,属于难题.

练习册系列答案
相关题目
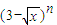 的展开式中x项的系数(n=2、3、4、…),则
的展开式中x项的系数(n=2、3、4、…),则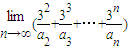 = .
= .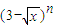 的展开式中x项的系数(n=2、3、4、…),则
的展开式中x项的系数(n=2、3、4、…),则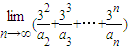 = .
= .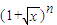 的展开式中x项的系数(n=2,3,4,…),则
的展开式中x项的系数(n=2,3,4,…),则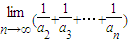 = .
= .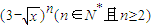 的展开式中x的系数,则
的展开式中x的系数,则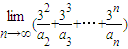 = .
= .