题目内容
已知
且
,现给出如下结论：
①
;②
;③
;④;
;
⑤
的极值为1和3.其中正确命题的序号为 .
②③
解析试题分析：依题意可得函数
.令
.所以函数在
和
上递增，在
递减，又，所以
.又
.由
可得，
.所以
（
）.又因为
.所以
.所以②③正确.若的极值为1和3，则可得
.即
与
矛盾，所以不成立.所以正确的选项是②③.
考点：1.函数的极值.2.函数与方程的根的问题.3.反证的数学思想.4.函数的单调性的应用.
练习册系列答案
相关题目
(
)的图象如图所示，则不等式
的解集为________．
，且函数
在
处有极值，则ab的最大值为 。
，过
可作曲线
的三条切线，则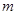
的取值范围是 ．
在点（1，2）处的切线经过坐标原点，则
= 
，若
，则x0的值为______．