题目内容
已知A={(x,y)|x(x-1)≤y(1-y)},B={(x,y)|x2+y2≤a}若A⊆B,则实数a的取值范围是
- A.(0,
 )
) - B.[
 ,+∞)
,+∞) - C.[2,+∞)
- D.[
 ,+∞)
,+∞)
C
分析:由题意,可先化简集合A,再它们表示的几何图形结合A⊆B即可判断出关于参数a的不等式,解出它的取值范围,即可选出正确选项.
解答: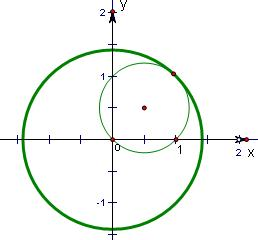 解:A={(x,y)|x(x-1)≤y(1-y)}={(x,y)|(x-
解:A={(x,y)|x(x-1)≤y(1-y)}={(x,y)|(x- )2+(y-
)2+(y- )2≤
)2≤ },
},
它表示圆心在( ),半径为
),半径为 的圆及其内部,
的圆及其内部,
B={(x,y)|x2+y2≤a}表示圆心在(0,0),半径为 的圆及其内部,
的圆及其内部,
又A⊆B,故大圆要包含小圆,如图.
当两圆内切时,a=2,
∴a≥2.
即实数a的取值范围是[2,+∞)
故选C.
点评:本题考点是集合关系中的参数取值问题,考查了集合的化简,集合的包含关系,解题的关键是熟练掌握集合包含关系的定义,由此得到参数所满足的不等式,本题考察了推理判断的能力,
分析:由题意,可先化简集合A,再它们表示的几何图形结合A⊆B即可判断出关于参数a的不等式,解出它的取值范围,即可选出正确选项.
解答:
 解:A={(x,y)|x(x-1)≤y(1-y)}={(x,y)|(x-
解:A={(x,y)|x(x-1)≤y(1-y)}={(x,y)|(x- )2+(y-
)2+(y- )2≤
)2≤ },
},它表示圆心在(
 ),半径为
),半径为 的圆及其内部,
的圆及其内部,B={(x,y)|x2+y2≤a}表示圆心在(0,0),半径为
 的圆及其内部,
的圆及其内部,又A⊆B,故大圆要包含小圆,如图.
当两圆内切时,a=2,
∴a≥2.
即实数a的取值范围是[2,+∞)
故选C.
点评:本题考点是集合关系中的参数取值问题,考查了集合的化简,集合的包含关系,解题的关键是熟练掌握集合包含关系的定义,由此得到参数所满足的不等式,本题考察了推理判断的能力,

练习册系列答案
相关题目