题目内容

（2012•兰州模拟）三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直，且长度分别为3、4、5，则三棱锥P-ABC外接球的表面积是
50π
50π
．
分析：以PA、PB、PC为过同一顶点的三条棱，作长方体如图，则长方体的外接球同时也是三棱锥P-ABC外接球．算出长方体的对角线即为球直径，结合球的表面积公式，可算出三棱锥P-ABC外接球的表面积．
解答：解：以PA、PB、PC为过同一顶点的三条棱，作长方体如图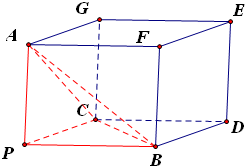
则长方体的外接球同时也是三棱锥P-ABC外接球．
∵长方体的对角线长为
PA2+PB2+PC2
=
32+42+52
=5
2

∴球直径为5
2
，半径R=
5
2
2

因此，三棱锥P-ABC外接球的表面积是4πR2=4π×（
5
2
2
）2=50π
故答案为：50π
点评：本题给出三棱锥的三条侧棱两两垂直，求它的外接球的表面积，着重考查了长方体对角线公式和球的表面积计算等知识，属于基础题．
练习册系列答案
相关题目
（2012•兰州模拟）若函数f(x)=sinωx+
3
cosωx，x∈R，又f（α）=f（β）=2，且|α-β|的最小值等于3π，则正数ω的值为（　　）
（2012•兰州模拟）双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)一条渐近线的倾斜角为
π
3
，离心率为e，则
a2+e
b
的最小值为
2
6
3
2
6
3
．
（2012•兰州模拟）某市为了推动全民健身运动在全市的广泛开展，该市电视台开办了健身竞技类栏目《健身大闯关》，规定参赛者单人闯关，参赛者之间相互没有影响，通过关卡者即可获奖．现有甲、乙、丙3人参加当天的闯关比赛，已知甲获奖的概率为
3
5
，乙获奖的概率为
2
3
，丙获奖而甲没有获奖的概率为
1
5
．
（1）求三人中恰有一人获奖的概率；
（2）记三人中至少有两人获奖的概率．
（2012•兰州模拟）若（1-2x）2012=a0+a1x+a2x2+…+a2012x2012，则
a1
2
+
a2
22
+…+
a2012
22012
=
-1
-1
．
（2012•兰州模拟）已知F为双曲线C：
x2
a2
-
y2
b2
=1(a＞0，b＞0)的右焦点，P为双曲线C右支上一点，且位于x轴上方，M为直线x=-
a2
c
上一点，O为坐标原点，已知
OP
=
OF
+
OM
，且|
OF
|=|
OM
|，则双曲线C的离心率为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网