Question

(本小题满分12分)

 

如图，在体积为1的三棱柱ABC－A1B1C1中，侧棱AA1⊥底面ABC，AB⊥AC，AC＝AA1=1，P为线段AB上的动点.

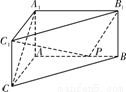
(1)求证：CA1⊥C1P；

(2)当AP为何值时，二面角C1－PB1－A1的大小为？

 

Answer 1

【答案】

 

（1）证明略

（2）2－

【解析】解：(1)证明：∵AA1⊥底面ABC，∴AA1⊥AC，AA1⊥AB.

又∵AB⊥AC，

∴以A为原点，AC，AB，AA1所在的直线分别为x轴，y轴，z轴建立直角坐标系.

又∵VABC－A1B1C1＝AB×AC×AA1＝1，∴AB＝2.(2分)

设AP＝m，则P(0，m,0)，而C1(1,0,1)，C(1,0,0)，A1(0,0,1)，

∴＝(－1,0,1)，＝(－1，m，－1)，

∴·＝(－1)×(－1)＋0×m＋1×(－1)＝0，

∴CA1⊥C1P.(6分)

(2)设平面C1PB1的一个法向量n＝(x，y，z)

令y＝1，则n＝(2,1，m－2)，(9分)

而平面A1B1P的一个法向量＝(1,0,0)，

依题意可知cos＝＝＝，

∴m＝2＋(舍去)或m＝2－.

∴当AP＝2－时，二面角C1－PB1－A1的大小为.(12分)