题目内容
设 是定义在
是定义在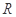 上的偶函数,对
上的偶函数,对 ,都有
,都有 ,且当
,且当 时,
时, ,若在区间
,若在区间 内关于
内关于 的方程
的方程 恰有3个不同的实数根,则
恰有3个不同的实数根,则 的取值范围是( )
的取值范围是( )
| A.(1,2) | B.(2,+∞) | C.(1, ) ) | D. |
D.
解析试题分析:因为对于任意的 ,都有
,都有 ,所以函数
,所以函数 的图象关于直线x=2对称,又因为当
的图象关于直线x=2对称,又因为当 时,
时, ,且函数
,且函数 是定义在R上的偶函数,若在区间
是定义在R上的偶函数,若在区间 内关于x的方程
内关于x的方程 恰有3个不同的实数解,则函数
恰有3个不同的实数解,则函数 与
与 在区间(-2,6)上有三个不同的交点,如下图所示:
在区间(-2,6)上有三个不同的交点,如下图所示:
又 ,则有
,则有 ,且
,且 ,解得
,解得 .
.
考点:1.指数函数与对数函数的图象与性质;2.函数的零点与方程根的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知 且
且 ,则下列不等式中成立的是 ( )
,则下列不等式中成立的是 ( )
A. |
B. |
C. |
D. |
定义在R上的奇函数 ,当
,当 时,
时, ,则函数
,则函数 的所有零点之和为( )
的所有零点之和为( )
A. | B. | C. | D. |
 等于( )
等于( )
| A.3 | B.4 | C.5 | D.6 |
下列判断正确的是( )
A. | B. | C. | D. |
设函数 的最小正周期为
的最小正周期为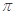 ,将
,将 的图象向左平移
的图象向左平移 个单位得函数
个单位得函数 的图象,则
的图象,则
A. 上单调递减 上单调递减 |
B. 上单调递减 上单调递减 |
C. 上单调递增 上单调递增 |
D. 上单调递增 上单调递增 |
 是定义域为
是定义域为 的偶函数,则函数
的偶函数,则函数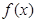 的单调递减区间是 .
的单调递减区间是 . )在映射
)在映射 下的象是
下的象是 ,则
,则 在
在 =____________.
=____________.