题目内容
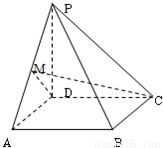
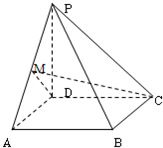
如图所示，已知PD⊥平面ABCD，底面ABCD是正方形，PD=AB，M是PA的中点，则二面角M-DC-A的大小为（ ）
A．
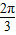
B．
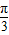
C．
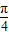
D．
【答案】分析：根据已知中PD⊥平面ABCD，底面ABCD是正方形，我们易判断出∠MDA即为二面角M-DC-A的平面角，再根据PD=AB，M是PA的中点，我们易根据等腰直角三角形的性质得到结果．
解答：
解：如图所示
∵PD⊥平面ABCD，CD?平面ABCD，
∴PD⊥CD，
又由底面ABCD是正方形，
∴CD⊥AD
∵AD∩PD=D
∴CD⊥平面PAD
则MD⊥CD
即∠MDA即为二面角M-DC-A的平面角
在Rt△PDA中，PD=AD，M是PA的中点，
∴∠MDA=
故选C
点评：本题考查的知识点是二面角的平面角的求法，解答的关键是求出二面角的平面角，将问题转化为一个解三角形问题．
解答：
解：如图所示∵PD⊥平面ABCD，CD?平面ABCD，
∴PD⊥CD，
又由底面ABCD是正方形，
∴CD⊥AD
∵AD∩PD=D
∴CD⊥平面PAD
则MD⊥CD
即∠MDA即为二面角M-DC-A的平面角
在Rt△PDA中，PD=AD，M是PA的中点，
∴∠MDA=
故选C
点评：本题考查的知识点是二面角的平面角的求法，解答的关键是求出二面角的平面角，将问题转化为一个解三角形问题．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，已知PD⊥平面ABCD，底面ABCD是正方形，PD=AB，M是PA的中点，则二面角M-DC-A的大小为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
，已知在矩形ABCD中，AB=1，BC=a（a＞0），PA⊥平面ABCD，且PA=1．
（2013•潮州二模）如图所示，已知AB为圆O的直径，点D为线段AB上一点，且AD=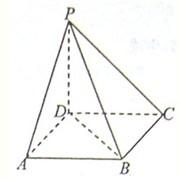
如图所示，已知ABCD是正方形，边长为2，PD⊥平面ABCD．