题目内容
已知函数f(x)=lnx,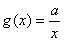 ,设F(x)=f(x)+g(x)。
,设F(x)=f(x)+g(x)。
(Ⅰ)当a=1时,求函数F(x)的单调区间;
(Ⅱ)若以函数y=F(x)(0<x≤3)图象上任意一点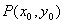 为切点的切线斜率
为切点的切线斜率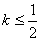 恒成立,求实数a的最小值。
恒成立,求实数a的最小值。
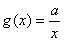 ,设F(x)=f(x)+g(x)。
,设F(x)=f(x)+g(x)。(Ⅰ)当a=1时,求函数F(x)的单调区间;
(Ⅱ)若以函数y=F(x)(0<x≤3)图象上任意一点
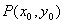 为切点的切线斜率
为切点的切线斜率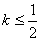 恒成立,求实数a的最小值。
恒成立,求实数a的最小值。 解:(Ⅰ)由已知,可得 ,
,
函数的定义域为 ,
,
则 ,
,
由 可得
可得 在区间
在区间 单调递增;
单调递增;
由 可得
可得 在(0,1)上单调递减。
在(0,1)上单调递减。
(Ⅱ)由题意,知 对任意
对任意 恒成立,
恒成立,
即有 对任意
对任意 恒成立,即
恒成立,即 ,
,
令 ,
,
即 ,
,
所以,实数a的最小值为 。
。
 ,
,函数的定义域为
 ,
,则
 ,
,由
 可得
可得 在区间
在区间 单调递增;
单调递增;由
 可得
可得 在(0,1)上单调递减。
在(0,1)上单调递减。(Ⅱ)由题意,知
 对任意
对任意 恒成立,
恒成立,即有
 对任意
对任意 恒成立,即
恒成立,即 ,
,令
 ,
,即
 ,
,所以,实数a的最小值为
 。
。
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目