题目内容
某同学为了研究函数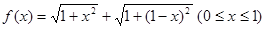 的性质,构造了如图所示的两个边长为
的性质,构造了如图所示的两个边长为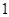 的正方形
的正方形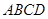 和
和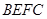 ,点
,点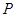 是边
是边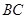 上的一个动点,设
上的一个动点,设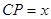 ,则
,则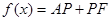 .那么可推知方程
.那么可推知方程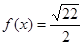 解的个数是( )
解的个数是( )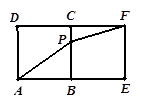
A. . . | B.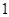 . . | C.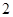 . . | D. . . |
C
解析试题分析:从图中知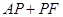 的最小值是
的最小值是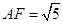 (当
(当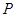 是
是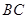 中点
中点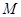 时取得),最大值是
时取得),最大值是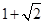 (当
(当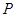 与
与 或
或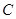 重合时取得),当
重合时取得),当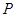 从点
从点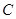 运动到点
运动到点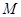 时
时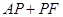 在递减,当
在递减,当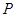 从点
从点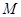 运动到点
运动到点 时
时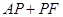 在递增,
在递增,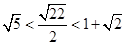 ,故使
,故使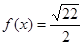 成立的
成立的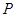 点有两个,即方程有两解.
点有两个,即方程有两解.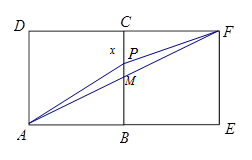
考点:函数的单调性.

练习册系列答案
相关题目
设a,b,c依次是方程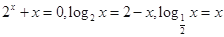 的根,则( )
的根,则( )
A.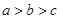 | B.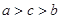 | C.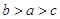 | D.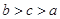 |
关于x的函数y=log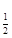 (a2-ax)在[0,+∞
(a2-ax)在[0,+∞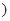 上为减函数,则实数a的取值范围是( ).
上为减函数,则实数a的取值范围是( ).
| A.(-∞,-1) | B.(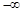 ,0) ,0) | C.(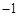 ,0) ,0) | D.(0,2 |
定义在R上的奇函数 满足
满足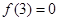 ,且不等式
,且不等式 在
在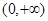 上恒成立,则函数
上恒成立,则函数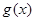 =
=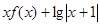 的零点的个数为( )
的零点的个数为( )
| A.4 | B.3 | C.2 | D.1 |
如图,直角坐标平面内的正六边形ABCDEF,中心在原点,边长为a,AB平行于x轴,直线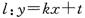 (k为常数)与正六边形交于M、N两点,记
(k为常数)与正六边形交于M、N两点,记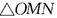 的面积为S,则关于函数
的面积为S,则关于函数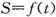 的奇偶性的判断正确的是 ( )
的奇偶性的判断正确的是 ( )
| A.一定是奇函数 |
| B.—定是偶函数 |
| C.既不是奇函数,也不是偶函数 |
| D.奇偶性与k有关 |
若函数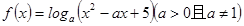 满足对任意的
满足对任意的 ,当
,当 时
时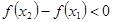 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B.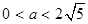 | C.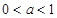 | D.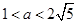 |
已知奇函数 在区间
在区间 上单调递减,则不等式
上单调递减,则不等式 的解集是( )
的解集是( )
A.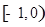 | B. | C. | D. |
 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当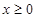 时,
时,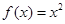 ,若对任意的
,若对任意的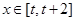 ,不等式
,不等式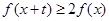 恒成立,则实数
恒成立,则实数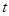 的取值范围是( )
的取值范围是( )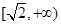
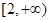
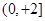
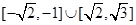
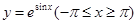 的大致图像为( )
的大致图像为( )