题目内容
已知正方体ABCD-A1B1C1D1的棱长为2,M、N分别为AA1、BB1的中点,求CM与D1N所成角的余弦值________.

分析:先建立空间直角坐标系,再写出相关点的坐标,得到异面直线方向向量的坐标,利用向量夹角公式计算所得向量夹角的余弦值,最后得异面直线所成角的余弦值,注意异面直线所成的角范围为(0,
 ],故面直线所成角的余弦值应为向量夹角的余弦值的绝对值.
],故面直线所成角的余弦值应为向量夹角的余弦值的绝对值.解答:如图,建立空间直角坐标系
 ,则A(0,0,0),C(2,2,0),M(0,0,1),N(2,0,1),D1(0,2,2)
,则A(0,0,0),C(2,2,0),M(0,0,1),N(2,0,1),D1(0,2,2)∴
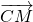 =(-2,-2,1),
=(-2,-2,1), =(2,-2,-1)
=(2,-2,-1)∴cos<
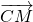 ,
, >=
>= =
= =-
=-
∵异面直线所成的角范围为(0,
 ]
]∴CM与D1N所成角的余弦值为

故答案为

点评:本题考察了异面直线所成的角的求法,利用空间直角坐标系和空间向量解决空间角的计算问题,将几何问题转化为代数问题的思想方法

练习册系列答案
相关题目
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1= 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.