题目内容
已知f(x)=ax+ +2-2a(a>0)在图象在点(1,f(1))处的切线与直线y=2x+1平行.
+2-2a(a>0)在图象在点(1,f(1))处的切线与直线y=2x+1平行.
(1)求a,b满足的关系式;
(2)若f(x)≥2lnx在[1,+∞)上恒成立,求a的取值范围;
(3)若a=1,数列{an}满足a1=2,an+1=f(an)+2-an(n∈N*),求证:a1•a2•a3…an=n+1.
(1)解:求导函数可得f′(x)=a-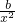 ,根据题意f′(1)=a-b=2,即b=a-2;
,根据题意f′(1)=a-b=2,即b=a-2;
(2)解:由(1)知,f(x)=ax+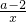 +2-2a,
+2-2a,
令g(x)=f(x)-2lnx=ax+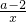 +2-2a-2lnx,x∈[1,+∞)
+2-2a-2lnx,x∈[1,+∞)
则g(1)=0,g′(x)=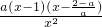
①当0<a<1时, ,若1<x<
,若1<x<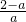 ,则g′(x)<0,g(x)在[1,+∞)减函数,所以g(x)<g(1)=0,即f(x)<2lnx在[1,+∞)上恒成立;
,则g′(x)<0,g(x)在[1,+∞)减函数,所以g(x)<g(1)=0,即f(x)<2lnx在[1,+∞)上恒成立;
②a≥1时,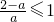 ,当x>1时,g′(x)>0,g(x)在[1,+∞)增函数,又g(1)=0,所以f(x)≥2lnx.
,当x>1时,g′(x)>0,g(x)在[1,+∞)增函数,又g(1)=0,所以f(x)≥2lnx.
综上所述,所求的取值范围是[1,+∞);
(3)证明:取a=1得f(x)=x- ,所以an+1=f(an)+2-an=2-
,所以an+1=f(an)+2-an=2-
∴an+1-1=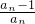 ,∴
,∴ =
= +1
+1
∴{ }是等差数列,首项为
}是等差数列,首项为 ,公差为1,
,公差为1,
∴ =n,∴
=n,∴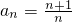
∴a1•a2•…an= •
• •…•
•…• =n+1.
=n+1.
分析:(1)求导函数,利用图象在点(1,f(1))处的切线与直线y=2x+1平行,可求a,b满足的关系式;
(2)构造g(x)=f(x)-2lnx,求导函数,分类讨论,确定函数的单调性,即可求得结论;
(3)取a=1得f(x)=x- ,利用an+1=f(an)+2-an=2-
,利用an+1=f(an)+2-an=2- ,可得{
,可得{ }是等差数列,首项为
}是等差数列,首项为 ,公差为1,从而可得数列通项,即可证得结论.
,公差为1,从而可得数列通项,即可证得结论.
点评:本题考查导数知识的运用,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.
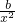 ,根据题意f′(1)=a-b=2,即b=a-2;
,根据题意f′(1)=a-b=2,即b=a-2;(2)解:由(1)知,f(x)=ax+
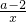 +2-2a,
+2-2a,令g(x)=f(x)-2lnx=ax+
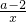 +2-2a-2lnx,x∈[1,+∞)
+2-2a-2lnx,x∈[1,+∞)则g(1)=0,g′(x)=
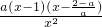
①当0<a<1时,
 ,若1<x<
,若1<x<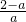 ,则g′(x)<0,g(x)在[1,+∞)减函数,所以g(x)<g(1)=0,即f(x)<2lnx在[1,+∞)上恒成立;
,则g′(x)<0,g(x)在[1,+∞)减函数,所以g(x)<g(1)=0,即f(x)<2lnx在[1,+∞)上恒成立;②a≥1时,
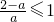 ,当x>1时,g′(x)>0,g(x)在[1,+∞)增函数,又g(1)=0,所以f(x)≥2lnx.
,当x>1时,g′(x)>0,g(x)在[1,+∞)增函数,又g(1)=0,所以f(x)≥2lnx.综上所述,所求的取值范围是[1,+∞);
(3)证明:取a=1得f(x)=x-
 ,所以an+1=f(an)+2-an=2-
,所以an+1=f(an)+2-an=2-
∴an+1-1=
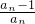 ,∴
,∴ =
= +1
+1∴{
 }是等差数列,首项为
}是等差数列,首项为 ,公差为1,
,公差为1,∴
 =n,∴
=n,∴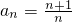
∴a1•a2•…an=
 •
• •…•
•…• =n+1.
=n+1.分析:(1)求导函数,利用图象在点(1,f(1))处的切线与直线y=2x+1平行,可求a,b满足的关系式;
(2)构造g(x)=f(x)-2lnx,求导函数,分类讨论,确定函数的单调性,即可求得结论;
(3)取a=1得f(x)=x-
 ,利用an+1=f(an)+2-an=2-
,利用an+1=f(an)+2-an=2- ,可得{
,可得{ }是等差数列,首项为
}是等差数列,首项为 ,公差为1,从而可得数列通项,即可证得结论.
,公差为1,从而可得数列通项,即可证得结论.点评:本题考查导数知识的运用,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目