题目内容
若直线2ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,则 的最小值是______.
的最小值是______.
- A.5
- B.6
- C.8
- D.9
D
分析:由圆的方程x2+y2+2x-4y+1=0?圆心O为(-1,2),半径r=2;又直线2ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4?(-1,2)为直线2ax-by+2=0(a>0,b>0)上的点,于是-2a-2b+2=0?a+b=1,代入 ,应用基本不等式即可.
,应用基本不等式即可.
解答:由x2+y2+2x-4y+1=0得:(x+1)2+(y-2)2=4,
∴该圆的圆心为O(-1,2),半径r=2;
又直线2ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,
∴直线2ax-by+2=0(a>0,b>0)经过圆心O(-1,2),
∴-2a-2b+2=0,即a+b=1,又a>0,b>0,
∴ =(
=( )•(a+b)=1+
)•(a+b)=1+ +
+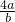 +4≥5+2
+4≥5+2 =9(当且仅当a=
=9(当且仅当a= ,b=
,b= 时取“=”).
时取“=”).
故选D.
点评:本题考查基本不等式,难点在于对“直线2ax-by+2=0(a>0,b>0)经过圆心O(-1,2),”的理解与应用,属于中档题.
分析:由圆的方程x2+y2+2x-4y+1=0?圆心O为(-1,2),半径r=2;又直线2ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4?(-1,2)为直线2ax-by+2=0(a>0,b>0)上的点,于是-2a-2b+2=0?a+b=1,代入
 ,应用基本不等式即可.
,应用基本不等式即可.解答:由x2+y2+2x-4y+1=0得:(x+1)2+(y-2)2=4,
∴该圆的圆心为O(-1,2),半径r=2;
又直线2ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,
∴直线2ax-by+2=0(a>0,b>0)经过圆心O(-1,2),
∴-2a-2b+2=0,即a+b=1,又a>0,b>0,
∴
 =(
=( )•(a+b)=1+
)•(a+b)=1+ +
+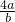 +4≥5+2
+4≥5+2 =9(当且仅当a=
=9(当且仅当a= ,b=
,b= 时取“=”).
时取“=”).故选D.
点评:本题考查基本不等式,难点在于对“直线2ax-by+2=0(a>0,b>0)经过圆心O(-1,2),”的理解与应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若直线2ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,则
+
的最小值是( )
| 1 |
| a |
| 2 |
| b |
A、4
| ||
B、3+2
| ||
C、3+2
| ||
D、4
|