Question

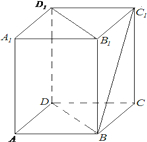（2012•张掖模拟）已知长方体ABCD-A₁B₁C₁D₁中，AB=BC=2，A₁D与BC₁所成的角为

π

2

，则BC₁与平面BB₁D₁D所成角的正弦值为（　　）

• A．

  6

  3

• B．

  1

  2

• C．

  15

  5

• D．

  3

  2

Answer 1

分析：根据已知中长方体ABCD-A₁B₁C₁D₁中，AB=BC=2，A₁D与BC₁所成角为90°，易判断这是一个棱长为2的正方体，设 O为B₁D₁的中点，证明C₁O⊥平面 BB₁D₁D，得出∠C₁BO为直线BC₁与平面BB₁D₁D所成角，解三角形∠C₁BO即可得到直线BC₁与平面BB₁D₁D所成角的大小．

解答：解：因为在长方体ABCD-A₁B₁C₁D₁中，AB=BC=2
∴上下底面为正方形
又∵BC₁∥AD₁，A₁D与BC₁所形成的角为90°，
∴A₁D与AD₁所成的角为90°，
∴AA₁D₁D为正方形，
∴ABCD-A₁B₁C₁D₁为正方体
设 O为B₁D₁的中点，则由C₁O⊥B₁D₁，C₁O⊥B₁B，
得出C₁O⊥平面 BB₁D₁D
连接BO，则∠C₁BO为直线BC₁与平面BB₁D₁D所成角
∵BC₁=2

2

； C₁O=

2

∴sin∠C₁BO=

1

2

∠C₁BO=30°
故选B．

点评：本题考查了直线与平面所成的角的概念与计算，考查空间想象能力、推理论证、计算能力．其中判断出棱柱为正方体且C₁BO为直线BC₁与平面BB₁D₁D所成角，是解答本题的关键．