题目内容
已知偶函数f（x）在区间[0，+∞）单调递增，则满足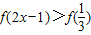
的x取值范围是（ ）A．
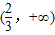
B．
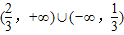
C．
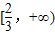
D．
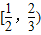
【答案】分析：当2x-1≥0时，直接根据函数的单调性，得不等式2x-1＞
；当2x-1＜0时，根据函数为偶函数的性质，将原不等式化为
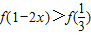，再由函数单调性得不等式1-2x
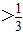．最后将两种情况的解集取并集，可得原不等式的解集．
解答：解：根据函数在区间[0，+∞）单调递增，得
当2x-1≥0，即x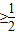
时，不等式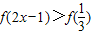
等价于2x-1＞
，解之得x＞
而当2x-1＜0，即x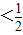
时，由于函数是偶函数，所以
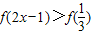等价于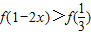
再根据单调性，得1-2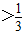x
，解之得x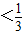
综上所述，不等式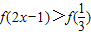
的解集为{x|x
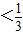或x＞
}
故选B
点评：本题给出抽象函数为偶函数且在[0，+∞）上为增函数，求关于x的不等式的解集，着重考查了函数单调性的奇偶性等知识，属于基础题．
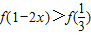；当2x-1＜0时，根据函数为偶函数的性质，将原不等式化为，再由函数单调性得不等式1-2x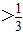．最后将两种情况的解集取并集，可得原不等式的解集．解答：解：根据函数在区间[0，+∞）单调递增，得
当2x-1≥0，即x
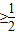时，不等式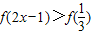等价于2x-1＞，解之得x＞而当2x-1＜0，即x
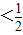时，由于函数是偶函数，所以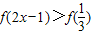等价于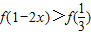再根据单调性，得1-2x
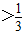，解之得x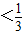综上所述，不等式
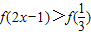的解集为{x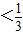|x或x＞}故选B
点评：本题给出抽象函数为偶函数且在[0，+∞）上为增函数，求关于x的不等式的解集，着重考查了函数单调性的奇偶性等知识，属于基础题．
练习册系列答案
相关题目
已知偶函数f（x）在区间[0，π]上单调递增，那么下列关系成立的是（ ）
A、f(-π)＞f(-2)＞f(
| ||
B、f(-π)＞f(-
| ||
C、f(-2)＞f(-
| ||
D、f(-
|