题目内容
在△ABC中,角A、B、C所对应的边分别为a、b、c,且满足2acosB=bcosC+ccosB.
(I)求角B的大小;
(II)求函数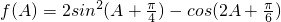 的最大值及取得最大值时的A值.
的最大值及取得最大值时的A值.
解:(Ⅰ)∵2acosB=bcosC+ccosB,由正弦定理 =
= =
= =2R得:
=2R得:
2sinAcosB=sinBcosC+cosBsinC…2′
即2sinAcosB=sin(B+C)=sinA,…4′
∴cosB= ,
,
∴B= …6′
…6′
(Ⅱ)f(A)=2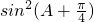 -cos(2A+
-cos(2A+ )
)
=1-cos(2A+ )-cos(2A+
)-cos(2A+ )
)
=1+sin2A- cos2A+
cos2A+ sin2A
sin2A
=1+ sin2A-
sin2A- cos2A
cos2A
=1+ sin(2A-
sin(2A- )…9′
)…9′
∵在△ABC中,B= ,
,
∴0<A< ,
,
∴- <2A-
<2A- <
< ,
,
∴当2A- =
= ,即A=
,即A= 时,f(A)取最大值.
时,f(A)取最大值.
∴f(A)max=1+ …12′
…12′
分析:(Ⅰ)由2acosB=bcosC+ccosB结合正弦定理可得cosB= ,从而可求角B的大小;
,从而可求角B的大小;
(Ⅱ)由降幂公式与辅助角公式可将f(A)整理为:f(A)=1+ sin(2A-
sin(2A- ),由B=
),由B= ,可求得0<A<
,可求得0<A< ,从而可求f(A)的最大值及取得最大值时的A值.
,从而可求f(A)的最大值及取得最大值时的A值.
点评:本题考查三角函数中的恒等变换及正弦定理的应用,突出降幂公式与辅助角公式的应用,属于中档题.
 =
= =
= =2R得:
=2R得:2sinAcosB=sinBcosC+cosBsinC…2′
即2sinAcosB=sin(B+C)=sinA,…4′
∴cosB=
 ,
,∴B=
 …6′
…6′(Ⅱ)f(A)=2
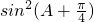 -cos(2A+
-cos(2A+ )
)=1-cos(2A+
 )-cos(2A+
)-cos(2A+ )
)=1+sin2A-
 cos2A+
cos2A+ sin2A
sin2A=1+
 sin2A-
sin2A- cos2A
cos2A=1+
 sin(2A-
sin(2A- )…9′
)…9′∵在△ABC中,B=
 ,
,∴0<A<
 ,
,∴-
 <2A-
<2A- <
< ,
,∴当2A-
 =
= ,即A=
,即A= 时,f(A)取最大值.
时,f(A)取最大值.∴f(A)max=1+
 …12′
…12′分析:(Ⅰ)由2acosB=bcosC+ccosB结合正弦定理可得cosB=
 ,从而可求角B的大小;
,从而可求角B的大小;(Ⅱ)由降幂公式与辅助角公式可将f(A)整理为:f(A)=1+
 sin(2A-
sin(2A- ),由B=
),由B= ,可求得0<A<
,可求得0<A< ,从而可求f(A)的最大值及取得最大值时的A值.
,从而可求f(A)的最大值及取得最大值时的A值.点评:本题考查三角函数中的恒等变换及正弦定理的应用,突出降幂公式与辅助角公式的应用,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |