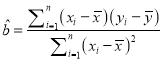题目内容
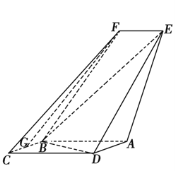
【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=![]() ,DE=3,∠BAD=60,G为BC的中点.
,DE=3,∠BAD=60,G为BC的中点.
(1)求证:FG![]() 平面BED;
平面BED;
(2)求证:平面BED⊥平面AED;
(3)求直线EF与平面BED所成角的正弦值.
【答案】见解析
【解析】(1)如图,取![]() 中点
中点![]() ,连接
,连接![]() ,在
,在![]() 中,因为
中,因为![]() 是
是![]() 中点,所以
中点,所以![]() 且
且![]() ,又因为
,又因为![]() ,所以
,所以![]() 且
且![]() ,即四边形
,即四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,(2分)
,(2分)
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .(3分)
.(3分)

(2)在![]() 中,
中,![]() °,由余弦定理可得
°,由余弦定理可得![]() ,进而得
,进而得![]() °,即
°,即![]() ,(5分)
,(5分)
又因为平面![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .(6分)
.(6分)
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .(7分)
.(7分)
(3)因为![]() ,所以直线
,所以直线![]() 与平面
与平面![]() 所成的角即为直线
所成的角即为直线![]() 与平面
与平面![]() 所成的角.过点
所成的角.过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,又平面
,又平面![]() 平面
平面![]() ,由(2)知
,由(2)知![]() 平面
平面![]() ,所以直线
,所以直线![]() 与平面
与平面![]() 所成的角即为
所成的角即为![]() .(9分)
.(9分)
在![]() 中,
中,![]() ,由余弦定理得
,由余弦定理得![]() ,所以
,所以![]() ,因此,
,因此,![]() ,在
,在![]() 中,
中,![]() ,所以直线EF与平面
,所以直线EF与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .(12分)
.(12分)

练习册系列答案
相关题目