题目内容
在△ABC中，a、b、c分别为角A、B、C的对边，已知向量
=（sinB，1-cosB）与向量
=（0，1） 的夹角为
，
求：（I） 角B 的大小； （Ⅱ） 
的取值范围．
解：（I）
，
，
，
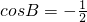∴0＜B＜π，
．
（II）由正弦定理得：
]=
∵
，∴
，∴
，
∴
，故的取值范围是（1，
．
分析：（I）由题意向量=（sinB，1-cosB）与向量=（0，1） 的夹角为，利用向量的夹角公式可以得到，解三角方程即可；
（II）由题意利用正弦定把这个式子化为角A的三角函数式子，利用角A的范围及三角函数知识即可求得．
点评：此题考查了两向量平行的坐标表示的从要条件，还考查了解三角方程，正弦定理，已知角的范围求三角函数的值域．
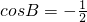，，，∴0＜B＜π，
．（II）由正弦定理得：
]=∵
，∴，∴，∴
，故的取值范围是（1，．分析：（I）由题意向量
=（sinB，1-cosB）与向量=（0，1） 的夹角为，利用向量的夹角公式可以得到，解三角方程即可；（II）由题意利用正弦定把
这个式子化为角A的三角函数式子，利用角A的范围及三角函数知识即可求得．点评：此题考查了两向量平行的坐标表示的从要条件，还考查了解三角方程，正弦定理，已知角的范围求三角函数的值域．
练习册系列答案
相关题目
在△ABC中，∠A、∠B、∠C所对的边长分别是a、b、c．满足2acosC+ccosA=b．则sinA+sinB的最大值是（ ）
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|