题目内容
7.如果双曲线过点(6,-2$\sqrt{2}$),它的两条渐近线方程x±2y=0,点A(a,0)(a>0)到双曲线上的点的最近距离为d.(1)求双曲线方程;
(2)求解析式d=f(a).
分析 (1)设双曲线的方程为x2-4y2=λ,利用双曲线过点(6,-2$\sqrt{2}$),求出λ,即可求双曲线方程;
(2)首先对a进行讨论①0<a≤2;②a>2,进一步求出点到双曲线距离的最小值.
解答 解:(1)设双曲线的方程为x2-4y2=λ
∵双曲线过点(6,-2$\sqrt{2}$),
∴36-4×8=λ,
∴λ=4,
∴双曲线方程为$\frac{1}{4}$x2-y2=1;
(2)双曲线:$\frac{1}{4}$x2-y2=1,若a>0,
①当0<a≤2时,点M(a,0)到双曲线的距离的最小值f(a)=2-a.
②当a>2时,点M(a,0)到双曲线的距离的最小值f(a)=a-2.
点评 本题考查的知识要点:双曲线的方程,分类讨论思想的应用,特殊位置的应用,属于中档题.

练习册系列答案
相关题目
17.已知集合A={1,2,3,4},B={x|x=2n,n∈A},则A∩B=( )
| A. | {1,4} | B. | {1,3} | C. | {2,4} | D. | {2,3} |
2.已知点A(-3,8),B(2,2),点P是x轴上的点,则当|AP|+|PB|最小时点P的坐标( )
| A. | (1,0) | B. | ($\frac{1}{2}$,0) | C. | ($\frac{1}{3}$,0) | D. | ($\frac{1}{4}$,0) |
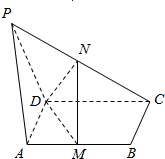 如图,PA⊥平面ABCD,ABCD是矩形,M、N分别是AB,PC的中点.
如图,PA⊥平面ABCD,ABCD是矩形,M、N分别是AB,PC的中点.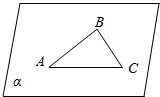 如图,在△ABC中,若AB,BC在平面α内,试判断AC是否在平面α内.
如图,在△ABC中,若AB,BC在平面α内,试判断AC是否在平面α内.