题目内容
△ABC中,三内角A,B,C成等差数列.
(1)若b=7,a+c=13,求此三角形的面积;
(2)求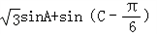 的取值范围.
的取值范围.
(1)若b=7,a+c=13,求此三角形的面积;
(2)求
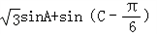 的取值范围.
的取值范围.解:因为A,B,C成等差数列,所以B=60°,
(1)由b2=a2+c2﹣2accos60°=(a+c)2﹣3ac,
即72=132﹣3ac,得ac=40,
所以△ABC的面积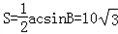 ;
;
(2)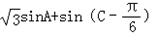 =
=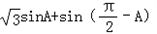
=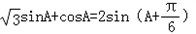
又由题可知A∈(0,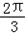 ),
),
所以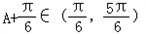 ,
,
所以sin(A+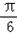 )∈(
)∈( ,1],
,1],
则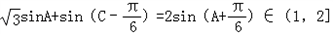 .
.
(1)由b2=a2+c2﹣2accos60°=(a+c)2﹣3ac,
即72=132﹣3ac,得ac=40,
所以△ABC的面积
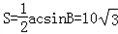 ;
;(2)
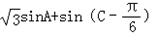 =
=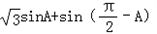
=
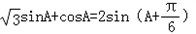
又由题可知A∈(0,
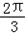 ),
),所以
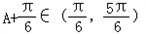 ,
,所以sin(A+
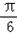 )∈(
)∈( ,1],
,1],则
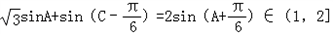 .
.
练习册系列答案
相关题目