Question

11．球O是四面体ABCD的外接球（即四面体的顶点均在球面上），若DB⊥平面ABC，AB⊥AC，且AC=1，DB=AB=2，则球O的表面积为9π．

Answer 1

分析 构造长方体，则长方体的外接球和四面体的外接球是相同的，由长方体的体对角线等于球的直径2R可求得2R=$\sqrt{{1}^{2}+{2}^{2}+{2}^{2}}$=3，从而求得R的值，即可求得球O的表面积．

解答 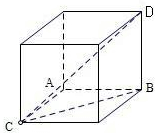解：∵DB⊥平面ABC，AB⊥AC，且AC=1，DB=AB=2，
∴构造长方体，则长方体的外接球和四面体的外接球是相同的，
则长方体的体对角线等于球的直径2R，
则2R=$\sqrt{{1}^{2}+{2}^{2}+{2}^{2}}$=3，
∴R=$\frac{3}{2}$，
则球O的表面积为4πR²=4π×（$\frac{3}{2}$）²=9π，
故答案是：9π．

点评 本题主要考查了直线与平面垂直的性质，球内接多面体，根据已知构造一个长方体是解题的关键，属于中档题．