题目内容
某工厂生产甲、乙两种产品，每种产品都有一部分是一等品，其余是二等品，已知甲产品为一等品的概率比乙产品为一等品的概率多0.25，甲产品为二等品的概率比乙产品为一等品的概率少0.05（1）分别求甲、乙产品为一等品的概率P甲，P乙；
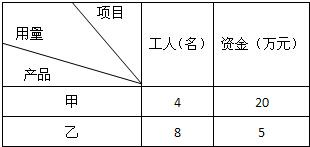
（2）已知生产一件产品需要用的工人数和资金数如右表所示，且该厂有工人32名，可用资金55万元．设x，y分别表示生产甲、乙产品的数量，在（1）的条件下，求x，y为何值时，z=xP甲+yP乙最大，最大值是多少？
分析：根据题意，列出相应的不等式组，作出不等式组对应的区域，根据目标函数的特征用线性规划的相关知识找到最优解．
解答：
解：（1）依题意得：
，
解得：
故甲产品为一等品的概率P甲=0.65，乙产品为一等品的概率P乙=0.4
（2）依题意得x，y应满足的约束条件为：
，
且z=0.65x+0.4y
作出以上不等式组所表示的平面区域（如图阴影部分），即可行域．
作直线l：0.65x+0.4y=0，即13x+8y=0，把直线l向上方平移到l1的位置时，直线经过可行域的点M，且l1与原点的距离最大，此时z取最大值．
解方程组
，得x=2，y=3
故M的坐标为（2，3），所以z的最大值为zmax=0.65×2+0.4×3=2.5
解：（1）依题意得：
|
解得：
|
故甲产品为一等品的概率P甲=0.65，乙产品为一等品的概率P乙=0.4
（2）依题意得x，y应满足的约束条件为：
|
且z=0.65x+0.4y
作出以上不等式组所表示的平面区域（如图阴影部分），即可行域．
作直线l：0.65x+0.4y=0，即13x+8y=0，把直线l向上方平移到l1的位置时，直线经过可行域的点M，且l1与原点的距离最大，此时z取最大值．
解方程组
|
故M的坐标为（2，3），所以z的最大值为zmax=0.65×2+0.4×3=2.5
点评：本题主要考查了等可能事件的概率、简单的线性规划，以及利用几何意义求最值，属于基础题．
练习册系列答案
相关题目
18、某工厂生产甲、乙两种产品，每种产品都是经过第一道和第二道工序加工而成，两道工序的加工结果相互独立，每道工序的加工结果均有A、B两个等级，对每种产品，两道工序的加工结果都为A级时，产品为一等品，其余均为二等品