Question

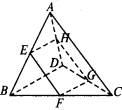
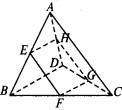
    如图，已知为平行四边形，，，，点在上，，，与相交于．现将四边形沿折起，使点在平面上的射影恰在直线上．

   （Ⅰ）求证：平面；

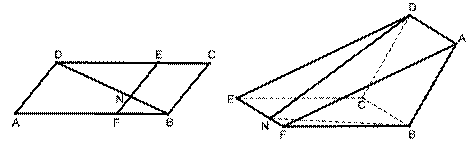   （Ⅱ）求折后直线DN与直线BF所成角的余弦值；

   （Ⅲ）求三棱锥N—ABF的体积．

Answer 1

解：（Ⅰ），得面

    则平面平面，

    由平面平面,

    则在平面上的射影在直线上,

    又在平面上的射影在直线上,

    则在平面上的射影即为点,

    故平面．         ……………4分

   （Ⅱ）法一．如图，建立空间直角坐标系，

    ∵在原图中AB=6，∠DAB=60°，

    则BN=，DN=2，∴折后图中BD=3，BC=3

    ∴N（0，，0），D（0，0，3），C（3，0，0）=（-1，0，0）

     ∴（-1，，0）（0，，-3）

    ∴=

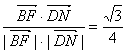
    ∴折后直线DN与直线BF所成角的余弦值为          ……………8分

    法二．在线段BC上取点M，使BM=BF，则MN∥BF

    ∴∠DNM或其补角为DN与BF所成角．

    又MN=BF=2，DM=．

    ∴

    ∴折后直线DN与直线BF所成角的余弦值为

   （Ⅲ）∵AD∥EF，   ∴A到平面BNF的距离等于D到平面BNF的距离，

    ∴

    即所求三棱锥的体积为           ……………12分