题目内容
(2007
重庆,20)已知函数,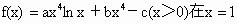 处取得极值―3―c,其中a,b,c为常数.
处取得极值―3―c,其中a,b,c为常数.
(1)
试确定a,b的值;(2)
讨论函数f(x)的单调区间;(3)
若对任意x>0,不等式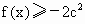 恒成立,求c的取值范围.
恒成立,求c的取值范围.
答案:略
解析:
提示:
解析:
|
解析: (1)由题意知f(1)=-3-c,因此 b-c=-3-c,从而b=-3.又对 f(x)求导得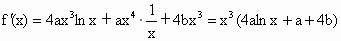 . .
由题意 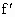 (1)=0,因此a+4b=0, (1)=0,因此a+4b=0,
解得 a=12.(2) 由(1)知 (x)= (x)= . .
令 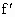 (x)=0,解得x=1. (x)=0,解得x=1.
当 0<x<1时,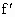 (x)<0,此时,f(x)为减函数; (x)<0,此时,f(x)为减函数;
当 x>1时,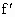 (x)>0,此时f(x)为增函数. (x)>0,此时f(x)为增函数.
因此 f(x)的单调递减区间为(0,1),而 f(x)的单调递增区间为(1,+∞).(3) 由(2)知,f(x)在x=1处取得极小值f(1)=-3-c,此极小值也是最小值,要使 f(x)≥-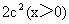 恒成立, 恒成立,
只需 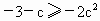 .即 .即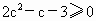 , ,
从而 (2c-3)(c+1)≥0.解得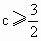 或c≤-1. 或c≤-1.
所以 c的取值范围为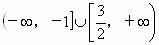 . . |
提示:
|
剖析:本题考查对数与对数函数及运用导数知识确定函数的单调性. |

练习册系列答案
相关题目