题目内容
已知函数f(x)=ax2+bx的图象过点(-4n,0),且f′(0)=2n(n∈N*).(1)求f(x)的解析式;
(2)若数列{an}满足![]() =f′(
=f′(![]() ),且a1=4,试求{an}的通项公式;
),且a1=4,试求{an}的通项公式;
(3)对(2)中数列{an},设Sn=a1+a2+…+an,求证:Sn<5.
(1)解:由f(x)的图象过(-4n,0),得b=4an.?
又f′(x)=2ax+b,由f′(0)=2n,得b=2n.?
所以a=![]() ,b=2n,即f(x)=
,b=2n,即f(x)=![]() x2+2nx. ?
x2+2nx. ?
(2)解:由![]() =f′(
=f′(![]() )得
)得![]() =
=![]() +2n,即
+2n,即![]() =
=![]() +2(n-1),?
+2(n-1),?
![]() =
=![]() +2(n-2),?
+2(n-2),?
……?
![]() =
=![]() +2×1,?
+2×1,?
叠加各式得![]() =
=![]() +2(1+2+…+n-1)?
+2(1+2+…+n-1)?
![]()
![]() =
=![]() +n(n-1).?
+n(n-1).?
所以an=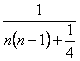 . ?
. ?
(3)证明:∵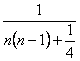 <
<![]() (n≥2), ?
(n≥2), ?
∴Sn=a1+a2+…+an<4+![]() +
+![]() +…+
+…+![]() ?
?
=4+(1-![]() )+(
)+(![]() -
-![]() )+…+(
)+…+(![]() -
-![]() )?
)?
=5-![]() <5.?
<5.?
故Sn<5.

练习册系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |