题目内容
 已知数列{an} 的各项全为正数,观察流程图,当k=2时,S=
已知数列{an} 的各项全为正数,观察流程图,当k=2时,S= ;当k=5 时,S=
;当k=5 时,S=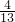 .
.
(1)写出k=4时,S的表达式;(用a1,a2,a3,a4,∧等表示)
(2)求{an} 的通项公式;
(3)令bn=2nan,求b1+b2+…+bn.
解:(1)当k=4时,S=


(2)由图知:数列an是一个等差数列,设公差为d,(d≠0)
当k=4时,S=


当k=4时,S=


∴ 解得:
解得:
∴an=3n-2.
(3)设Tn=b1+b2+…+bn.
则Tn=1•21+4•22+…+(3n-2)•2n,
2Tn=1•22+4•23+…+(3n-2)•2n+1,
两式相减得:-Tn=1•21+3•22+…+3•2n-(3n-2)•21+n,
∴Tn=(3n-5)•2n+1+10.
分析:(1)经过分析,程序框图为当型循环结构,按照框图题意分析求出当k=4时,S的值;{an}的通项.
(2)由图知:数列an是一个等差数列,设公差为d,(d≠0)求出{an}的通项邓可.
(3)根据(2)的结论,得到bn=(3n-2)•2n,然后代入求b1+b2+…+bm的值利用错位相消法求和即可
点评:本题考查程序框图,数列的概念及简单表示方法,数列的求和,通过对知识的熟练把握,分别进行求值,属于基础题.



(2)由图知:数列an是一个等差数列,设公差为d,(d≠0)
当k=4时,S=



当k=4时,S=



∴
 解得:
解得:
∴an=3n-2.
(3)设Tn=b1+b2+…+bn.
则Tn=1•21+4•22+…+(3n-2)•2n,
2Tn=1•22+4•23+…+(3n-2)•2n+1,
两式相减得:-Tn=1•21+3•22+…+3•2n-(3n-2)•21+n,
∴Tn=(3n-5)•2n+1+10.
分析:(1)经过分析,程序框图为当型循环结构,按照框图题意分析求出当k=4时,S的值;{an}的通项.
(2)由图知:数列an是一个等差数列,设公差为d,(d≠0)求出{an}的通项邓可.
(3)根据(2)的结论,得到bn=(3n-2)•2n,然后代入求b1+b2+…+bm的值利用错位相消法求和即可
点评:本题考查程序框图,数列的概念及简单表示方法,数列的求和,通过对知识的熟练把握,分别进行求值,属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目