题目内容
已知函数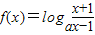 (a>0,a≠1).
(a>0,a≠1).(1)判断函数f(x)的奇偶性;
(2)判断函数f(x)在(1,+∞)上的单调性,并给出证明;
(3)当x∈(n,a-2)时,函数f(x)的值域是(1,+∞),求实数a与n的值.
【答案】分析:(1)先求函数的定义域看是否关于原点对称,然后在用奇偶函数的定义判断,要注意到代入-x时,真数是原来的倒数,这样就不难并判断奇偶性.
(2)用单调性的定义进行证明,首先在所给的区间上任取两个自变量看真数的大小关系,然后在根据底的不同判断函数单调性.
(3)要根据第二问的结论,进行分类讨论,解出两种情况下的实数a与n的值.
解答:解:(1)由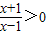 得函数f(x)的定义域为(1,+∞)∪(-∞,-1),…(2分)
得函数f(x)的定义域为(1,+∞)∪(-∞,-1),…(2分)
又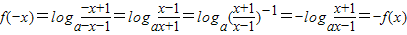
所以f(x)为奇函数. …(4分)
(2)由(1)及题设知: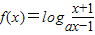 ,设
,设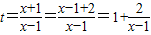 ,
,
∴当x1>x2>1时,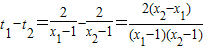 ∴t1<t2.…(6分)
∴t1<t2.…(6分)
当a>1时,logat1<logat2,即f(x1)<f(x2).
∴当a>1时,f(x)在(1,+∞)上是减函数.
同理当0<a<1时,f(x)在(1,+∞)上是增函数.…(8分)
(3)①当n<a-2≤-1时,有0<a<1.
由(2)可知:f(x)在(n,a-2)为增函数,…(9分)
由其值域为(1,+∞)知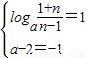 ,无解 …(11分)
,无解 …(11分)
②当1≤n<a-2时,有a>3.由(2)知:f(x)在(n,a-2)为减函数,
由其值域为(1,+∞)知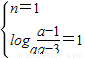 …(13分)
…(13分)
得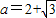 ,n=1.…(14分)
,n=1.…(14分)
点评:本题主要考查了对数型函数的奇偶性和单调性的判断,要先看真数部分在看整体的先后顺序进行,还要注意对底数的讨论,总体来说本题很基础、很典型,是不得不练的好题.
(2)用单调性的定义进行证明,首先在所给的区间上任取两个自变量看真数的大小关系,然后在根据底的不同判断函数单调性.
(3)要根据第二问的结论,进行分类讨论,解出两种情况下的实数a与n的值.
解答:解:(1)由
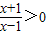 得函数f(x)的定义域为(1,+∞)∪(-∞,-1),…(2分)
得函数f(x)的定义域为(1,+∞)∪(-∞,-1),…(2分)又
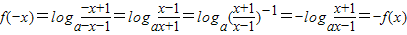
所以f(x)为奇函数. …(4分)
(2)由(1)及题设知:
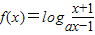 ,设
,设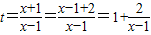 ,
,∴当x1>x2>1时,
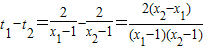 ∴t1<t2.…(6分)
∴t1<t2.…(6分)当a>1时,logat1<logat2,即f(x1)<f(x2).
∴当a>1时,f(x)在(1,+∞)上是减函数.
同理当0<a<1时,f(x)在(1,+∞)上是增函数.…(8分)
(3)①当n<a-2≤-1时,有0<a<1.
由(2)可知:f(x)在(n,a-2)为增函数,…(9分)
由其值域为(1,+∞)知
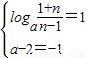 ,无解 …(11分)
,无解 …(11分)②当1≤n<a-2时,有a>3.由(2)知:f(x)在(n,a-2)为减函数,
由其值域为(1,+∞)知
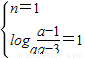 …(13分)
…(13分)得
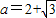 ,n=1.…(14分)
,n=1.…(14分)点评:本题主要考查了对数型函数的奇偶性和单调性的判断,要先看真数部分在看整体的先后顺序进行,还要注意对底数的讨论,总体来说本题很基础、很典型,是不得不练的好题.

练习册系列答案
相关题目
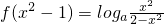 (a>0且a≠1).
(a>0且a≠1). (a>0,a≠1)的图象恒过定点A,若点A也在函数f(x)=3x+b的图象上,则b= .
(a>0,a≠1)的图象恒过定点A,若点A也在函数f(x)=3x+b的图象上,则b= . 其中a>0,且a≠1,
其中a>0,且a≠1, 的定义域;
的定义域; ;
; 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. =loga
=loga (a>0且a≠1)是奇函数
(a>0且a≠1)是奇函数 ,(
,(