题目内容

已知数列a_n中，a_n≠0，a₁=1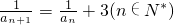， $数学公式$ ，则a₁₀的值为

A.
28
B.
33
C.
$数学公式$
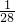
D.
$数学公式$

C
分析：根据题意可得， $\text{[math]}$ - $\text{[math]}$ =3，分析可得{ $\text{[math]}$ }是以 $\text{[math]}$ =1为首项，3为公差的等差数列；从而由等差数列的通项公式可得 $\text{[math]}$ 的值，进而可得答案．
解答：根据题意，可得 $\text{[math]}$ - $\text{[math]}$ =3，
则{ $\text{[math]}$ }是以 $\text{[math]}$ =1为首项，3为公差的等差数列；
则 $\text{[math]}$ = $\text{[math]}$ +（10-1）×3=28；
则a₁₀= $\text{[math]}$ ；
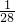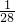故选C．
点评：本题考查数列的递推公式的运用，要掌握常见的由递推公式求通项公式或发现数列规律的常见方法．

练习册系列答案

好课堂堂练系列答案

基本功训练系列答案

我能考第一金牌一课一练系列答案

新课标同步单元练习系列答案

满分王周周检测系列答案

同步精练广东系列答案

全程导练提优训练系列答案

手拉手全优练考卷系列答案

第一好卷冲刺100分系列答案

新课改新学案系列答案

相关题目

已知数列a_n中，a₁=

，点（n，2a_n+1，-a_n）在直线y=x上，其中n=l，2，3，…．（1）令b_n=a_n+1-a_n-1，证明数列b_n是等比数列；（2）求数列a_n的前n项和S_n．

已知数列a_n中，a₁=1，a₂=a-1（a≠1，a为实常数），前n项和S_n恒为正值，且当n≥2时，

．
（1）求证：数列S_n是等比数列；
（2）设a_n与a_n+2的等差中项为A，比较A与a_n+1的大小；
（3）设m是给定的正整数，a=2．现按如下方法构造项数为2m有穷数列b_n：当k=m+1，m+2，…，2m时，b_k=a_k•a_k+1；当k=1，2，…，m时，b_k=b_2m-k+1．求数列{b_n}的前n项和为T_n（n≤2m，n∈N^*）．

已知数列a_n=2n-1，数列{b_n}的前n项和为T_n，满足T_n=1-b_n
（I）求{b_n}的通项公式；
（II）在{a_n}中是否存在使得

是{b_n}中的项，若存在，请写出满足题意的一项（不要求写出所有的项）；若不存在，请说明理由．

已知数列a_n中，a_n≠0，a₁=1，

+3(n∈N*)，则a₁₀的值为（　　）

已知数列a_n=2n-1，数列{b_n}的前n项和为T_n，满足T_n=1-b_n
（I）求{b_n}的通项公式；
（II）在{a_n}中是否存在使得 $数学公式$ 是{b_n}中的项，若存在，请写出满足题意的一项（不要求写出所有的项）；若不存在，请说明理由．