题目内容
已知各项均为正数的数列{an}满足an+12-an+1an-2an2=0,且a3+2是a2,a4的等差中项。
(1)求数列{an}的通项公式;
(2)若bn=an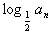 ,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整数n的最小值。
,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整数n的最小值。
(1)求数列{an}的通项公式;
(2)若bn=an
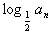 ,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整数n的最小值。
,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整数n的最小值。解:(1)∵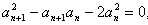
∴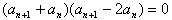
∵数列{an}的各项均为正数,
∴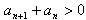
∴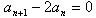
即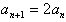
所以数列{an}是以2为公比的等比数列
∵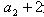 是
是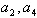 的等差中项
的等差中项
∴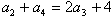
∴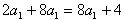
∴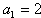
∴数列{an}的通项公式an=2n;
(2)由(1)及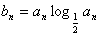 得
得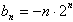
∵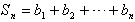
∴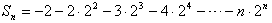 ①
①
∴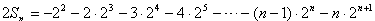 ②
②
①-②得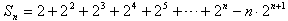
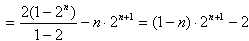
要使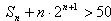 成立,只需
成立,只需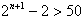 成立
成立
即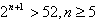
使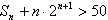 成立的正整数n的最小值为5。
成立的正整数n的最小值为5。
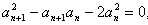
∴
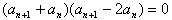
∵数列{an}的各项均为正数,
∴
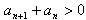
∴
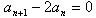
即
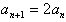
所以数列{an}是以2为公比的等比数列
∵
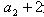 是
是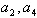 的等差中项
的等差中项∴
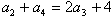
∴
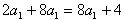
∴
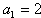
∴数列{an}的通项公式an=2n;
(2)由(1)及
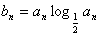 得
得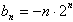
∵
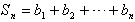
∴
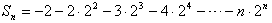 ①
①∴
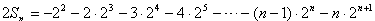 ②
②①-②得
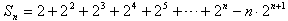
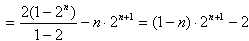
要使
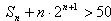 成立,只需
成立,只需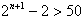 成立
成立即
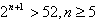
使
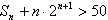 成立的正整数n的最小值为5。
成立的正整数n的最小值为5。
练习册系列答案
相关题目
 与
与 的大小,并加以证明.
的大小,并加以证明. 与
与 的大小,并加以证明.
的大小,并加以证明. 与
与 的大小,并加以证明.
的大小,并加以证明.