题目内容
（2011•山东）设A1，A2，A3，A4是平面直角坐标系中两两不同的四点，若
（λ∈R），
（μ∈R），且
，则称A3，A4调和分割A1，A2，已知点C（c，0），D（d，O）（c，d∈R）调和分割点A（0，0），B（1，0），则下面说法正确的是（ ）
| A．C可能是线段AB的中点 |
| B．D可能是线段AB的中点 |
| C．C，D可能同时在线段AB上 |
| D．C，D不可能同时在线段AB的延长线上 |
D
解析
练习册系列答案
相关题目
在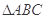
中，若
，则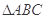一定是（ ）.
| A．钝角三角形 | B．锐角三角形 | C．直角三角形 | D．不能确定 |
下列结论中，正确结论的个数是（ ）
（1）若
，且
，则
（2）
（3）
（4）若
,
,
，
，
则
或
| A．0 | B．1 | C．2 | D．3 |
已知向量a，b满足|a|＝1，|a＋b|＝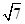
，〈a，b〉＝
，则|b|＝( )
| A．2 | B．3 | C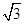． | D．4 |
(2014·孝感模拟)已知下列结论：
①若a=b,b=c,则a=c;
②若a∥b,b∥c,则a∥c;
③|a·b|=|a|·|b|;
④若a·b=a·c,则b=c的逆命题.
其中正确的是( )
| A．①② | B．①④ | C．①②③ | D．①②④ |
已知向量
=（3，0），
=（0，1），若
与
共线，则实数的λ值为（ ）
| A．1 | B．﹣1 | C． | D． |
（2013•浙江）设△ABC，P0是边AB上一定点，满足
，且对于边AB上任一点P，恒有
则（ ）
| A．∠ABC=90° | B．∠BAC=90° | C．AB=AC | D．AC=BC |
设a、b为不共线的非零向量，
，
，
，那么
为( )
A． |
B． |
C． |
D． |
如图，△ABC中，∠A＝60°，∠A的平分线交BC于D，若AB＝4，且
＝
＋λ
(λ∈R)，则AD的长为( )
A．2 | B．3 | C．4 | D．5 |