题目内容
设x1,x2…,xn∈R+,求证:
+
+…+
+
≥x1+x2+…+xn.
| x12 |
| x2 |
| x22 |
| x3 |
| xn-12 |
| xn |
| ||
| x1 |
分析:利用基本不等式,再相加,即可得出结论.
解答:证明:∵x1,x2…,xn∈R+,
∴
+x2≥2x1,
+x3≥2x2,…,
+x1≥2xn,
相加可得
+x2+
+x3+…+
+x1≥2x1+2x2+…+2xn,
∴
+
+…+
+
≥x1+x2+…+xn.
∴
| x12 |
| x2 |
| x22 |
| x3 |
| xn2 |
| x1 |
相加可得
| x12 |
| x2 |
| x22 |
| x3 |
| xn2 |
| x1 |
∴
| x12 |
| x2 |
| x22 |
| x3 |
| xn-12 |
| xn |
| ||
| x1 |
点评:本题考查不等式的证明,考查基本不等式的运用,正确运用基本不等式是关键.

练习册系列答案
相关题目
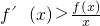 ,
,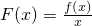 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;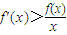 ,
,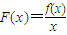 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;