题目内容
(本小题满分15分)
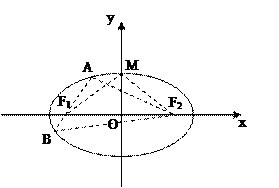
如图,椭圆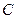 的中心在原点,焦点在
的中心在原点,焦点在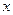 轴上,
轴上,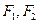 分别是椭圆
分别是椭圆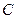 的左、右焦点,
的左、右焦点,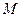 是椭圆短轴的一个端点,过
是椭圆短轴的一个端点,过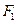 的直线
的直线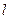 与椭圆交于
与椭圆交于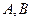 两点,
两点,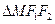 的面积为
的面积为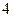 ,
,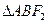 的周长为
的周长为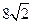 .
.
(1)求椭圆 的方程;
的方程;
(2)设点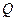 的坐标为
的坐标为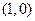 ,是否存在椭圆上的点
,是否存在椭圆上的点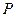 及以
及以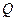 为圆心的一个圆,使得该圆与直线
为圆心的一个圆,使得该圆与直线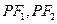 都相切,如存在,求出
都相切,如存在,求出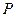 点坐标及圆的方程,如不存在,请说明理由.
点坐标及圆的方程,如不存在,请说明理由.
如图,椭圆
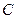 的中心在原点,焦点在
的中心在原点,焦点在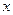 轴上,
轴上,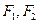 分别是椭圆
分别是椭圆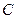 的左、右焦点,
的左、右焦点,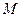 是椭圆短轴的一个端点,过
是椭圆短轴的一个端点,过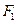 的直线
的直线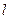 与椭圆交于
与椭圆交于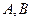 两点,
两点,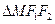 的面积为
的面积为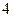 ,
,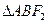 的周长为
的周长为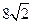 .
.
(1)求椭圆
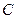 的方程;
的方程;(2)设点
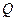 的坐标为
的坐标为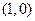 ,是否存在椭圆上的点
,是否存在椭圆上的点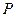 及以
及以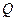 为圆心的一个圆,使得该圆与直线
为圆心的一个圆,使得该圆与直线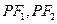 都相切,如存在,求出
都相切,如存在,求出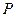 点坐标及圆的方程,如不存在,请说明理由.
点坐标及圆的方程,如不存在,请说明理由.(Ⅰ) 由题意知:
 ,解得
,解得 
∴ 椭圆的方程为 ……… 6分
……… 6分
(Ⅱ)假设存在椭圆上的一点 ,使得直线
,使得直线 与以
与以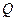 为圆心的圆相切,
为圆心的圆相切,
则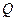 到直线
到直线 的距离相等,
的距离相等,
 :
: 
 :
:  ……… 8分
……… 8分
 ……… 9分
……… 9分
化简整理得: ……… 10分
……… 10分
∵ 点在椭圆上,∴
解得: 或
或  (舍) …… 13分
(舍) …… 13分
 时,
时, ,
, ,
,
∴ 椭圆上存在点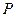 ,其坐标为
,其坐标为 或
或 ,使得直线
,使得直线 与以
与以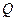 为圆心的圆
为圆心的圆 相切 ……… 15分
相切 ……… 15分

 ,解得
,解得 
∴ 椭圆的方程为
 ……… 6分
……… 6分(Ⅱ)假设存在椭圆上的一点
 ,使得直线
,使得直线 与以
与以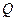 为圆心的圆相切,
为圆心的圆相切,则
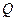 到直线
到直线 的距离相等,
的距离相等,
 :
: 
 :
:  ……… 8分
……… 8分 ……… 9分
……… 9分化简整理得:
 ……… 10分
……… 10分∵ 点在椭圆上,∴

解得:
 或
或  (舍) …… 13分
(舍) …… 13分 时,
时, ,
, ,
, ∴ 椭圆上存在点
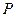 ,其坐标为
,其坐标为 或
或 ,使得直线
,使得直线 与以
与以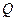 为圆心的圆
为圆心的圆 相切 ……… 15分
相切 ……… 15分略

练习册系列答案
相关题目
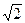 ),且离心率e满足:
),且离心率e满足: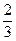 ,e,
,e,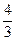 成等比数列.
成等比数列.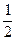
 求出l的倾斜角的范围;若不存在,请说明理由.
求出l的倾斜角的范围;若不存在,请说明理由.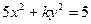 的一个焦点是
的一个焦点是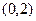 ,那
,那 么
么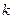 等于( )
等于( )
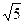 D
D 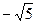
 ,则焦点坐标为 ( )
,则焦点坐标为 ( )







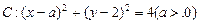 及直线l:x-y+3=O,当直线l被圆C截得的
及直线l:x-y+3=O,当直线l被圆C截得的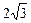 时,则a=( )
时,则a=( )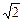
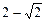
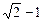
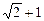
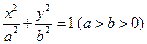 的
的 左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴, 直线AB交
左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴, 直线AB交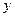 轴于点P,若
轴于点P,若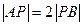 ,则椭圆的离心率是( )
,则椭圆的离心率是( )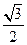

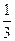
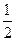
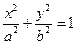 (a>b>0)的
(a>b>0)的 离心率为
离心率为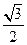 ,过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A、B两点,若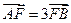 。则
。则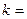 ( )
( ) 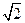 (D)
(D)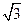
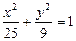 的焦点F1 、F2,P为椭圆上的一点,已知
的焦点F1 、F2,P为椭圆上的一点,已知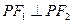 ,则
,则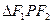
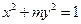 的离心率为
的离心率为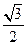 ,则它的长半轴长为_______________
,则它的长半轴长为_______________