题目内容
如图，圆锥SO中，AB、CD为底面圆的两条直径，AB∩CD=O，且AB⊥CD，SO=OB=2，P为SB的中点．异面直线SA与PD所成角的正切值为 ．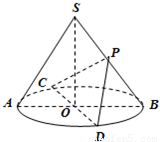
【答案】分析：由于SA与PD是异面直线，所以需要平移为相交直线才可以找到异面直线SA与PD所成角，因此连接OP在利用中位线可达到这一目的．
解答：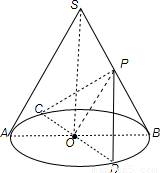
解：连接OP则OP 
SA，故∠OPD即为SA与PD的夹角．
∵SO=OB=2∴SA=
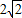∴OP=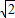
又在△PCD中PO⊥CD∴在Rt△POD中OD=2，OP=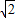
∴tan＜SA，PD＞=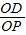
=
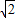
故答案为：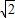
点评：此题关键是构造出△PCD并且利用圆锥的对称性得到△PCD为直角三角形进而求解．
解答：
解：连接OP则OP SA，故∠OPD即为SA与PD的夹角．∵SO=OB=2∴SA=
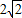∴OP=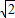又在△PCD中PO⊥CD∴在Rt△POD中OD=2，OP=
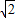
∴tan＜SA，PD＞=
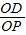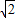
=故答案为：
点评：此题关键是构造出△PCD并且利用圆锥的对称性得到△PCD为直角三角形进而求解．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
