题目内容
已知函数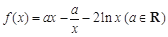 .
.
(Ⅰ)若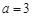 ,求曲线
,求曲线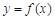 在点
在点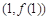 处的切线方程;
处的切线方程;
(Ⅱ)求函数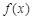 的单调区间;
的单调区间;
(Ⅲ)设函数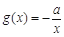 .若至少存在一个
.若至少存在一个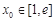 ,使得
,使得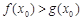 成立,求实数
成立,求实数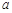 的取值范围.
的取值范围.
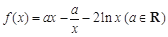 .
.(Ⅰ)若
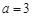 ,求曲线
,求曲线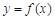 在点
在点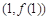 处的切线方程;
处的切线方程;(Ⅱ)求函数
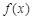 的单调区间;
的单调区间;(Ⅲ)设函数
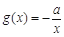 .若至少存在一个
.若至少存在一个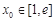 ,使得
,使得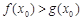 成立,求实数
成立,求实数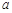 的取值范围.
的取值范围.(1)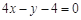
(2)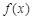 的单调递增区间为
的单调递增区间为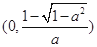 和
和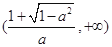 ,单调递减区间为
,单调递减区间为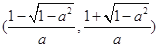
(3)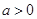
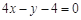
(2)
 的单调递增区间为
的单调递增区间为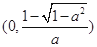 和
和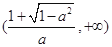 ,单调递减区间为
,单调递减区间为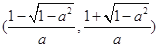
(3)
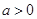
试题分析:函数的定义域为
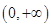 , 1分
, 1分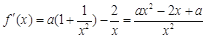 . 2分
. 2分(Ⅰ)当
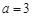 时,函数
时,函数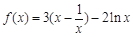 ,
,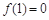 ,
,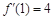 .
.所以曲线
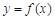 在点
在点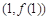 处的切线方程为
处的切线方程为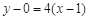 ,
,即
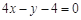 . 4分
. 4分(Ⅱ)函数
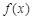 的定义域为
的定义域为 .
. (i)当
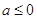 时,
时, 在
在 上恒成立,
上恒成立,则
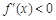 在
在 上恒成立,此时
上恒成立,此时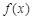 在
在 上单调递减. 5分
上单调递减. 5分(2)当
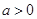 时,
时,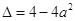 ,
,(ⅰ)若
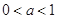 ,
,由
 ,即
,即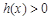 ,得
,得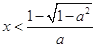 或
或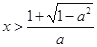 ; 6分
; 6分由
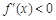 ,即
,即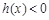 ,得
,得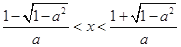 . 7分
. 7分所以函数
 的单调递增区间为
的单调递增区间为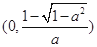 和
和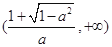 ,
,单调递减区间为
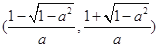 . 8分
. 8分(ⅱ)若
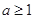 ,
,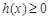 在
在 上恒成立,则
上恒成立,则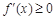 在
在 上恒成立,此时
上恒成立,此时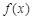 在
在 上单调递增. 9分
上单调递增. 9分(Ⅲ))因为存在一个
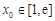 使得
使得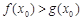 ,
,则
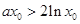 ,等价于
,等价于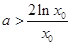 . 10分
. 10分令
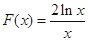 ,等价于“当
,等价于“当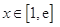 时,
时,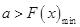 ”.
”. 对
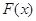 求导,得
求导,得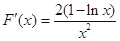 . 11分
. 11分因为当
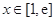 时,
时,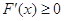 ,所以
,所以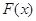 在
在 上单调递增. 12分
上单调递增. 12分所以
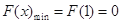 ,因此
,因此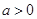 . 13分
. 13分点评:主要是考查了导数在研究函数中的运用,属于基础题。

练习册系列答案
相关题目
 与
与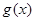 和区间D,如果存在
和区间D,如果存在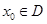 ,使
,使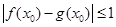 ,则称
,则称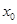 是函数
是函数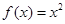 ,
, ②
②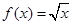 ,
,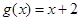
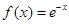 ,
,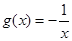 ④
④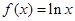 ,
,
 上存在“友好点”的有( )
上存在“友好点”的有( )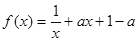 ,
,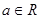 ,
,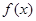 为奇函数,求
为奇函数,求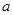 的值;
的值;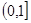 上是减函数;
上是减函数;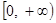 上的最小值.
上的最小值. 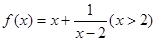 在
在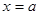 处取最小值, 则
处取最小值, 则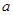 =( )
=( )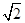
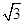
 的定义域为
的定义域为 ,
, 时,求函数
时,求函数 的最大值。
的最大值。 (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度 (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当 (千克/年);当
(千克/年);当 时,
时, (尾/立方米)时,因缺氧等原因,
(尾/立方米)时,因缺氧等原因, (千克/年).
(千克/年). 时,求函数
时,求函数 的表达式;
的表达式; 可以达到最大,并求出最大值.
可以达到最大,并求出最大值. 是函数
是函数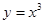 的极值点;
的极值点;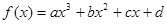 有极值点的充要条件是
有极值点的充要条件是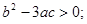
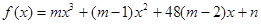 在区间
在区间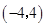 上单调递减.
上单调递减.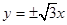 ,则其离心率为2.
,则其离心率为2.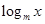 (m为常数0<m<1),且数列{f(
(m为常数0<m<1),且数列{f( )}是首项为2,公差为2的等差数列.
)}是首项为2,公差为2的等差数列.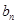 =
=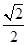 时,求数列{
时,求数列{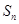 ;
; =
=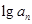 ,如果{
,如果{