Question

设F是抛物线G：:x²=4y的焦点.

（Ⅰ）过点P（0，－4）作抛物线G的切线，求切线方程：

（Ⅱ）设A、B为抛物线G上异于原点的两点，且满足,延长AF、BF分别交抛物线G于点C,D，求四边形ABCD面积的最小值.

Answer 1

本小题主要考查抛物线的方程与性质，抛物线的切点与焦点，向量的数量积，直线与抛物线的位置关系，平均不等式等基础知识，考查综合分析问题、解决问题的能力．

解：（I）设切点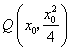．由，知抛物线在点处的切线斜率为，故所求切线方程为．

即．

因为点在切线上．

所以，，．

所求切线方程为．

（II）设，．

由题意知，直线的斜率存在，由对称性，不妨设．

因直线过焦点，所以直线的方程为．

点的坐标满足方程组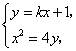

得，

由根与系数的关系知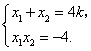

．

因为，所以的斜率为，从而的方程为．

同理可求得．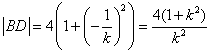

．

当时，等号成立．所以，四边形面积的最小值为．