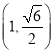Question

【题目】在△ABC中，角A、B、C所对的边长分别为a、b、c，且acosB+bcosA＝2ccosB．

（1）若a＝3，，求c的值；

（2）若，求f（A）的取值范围．

Answer 1

【答案】（1）c＝1或c＝2；（2）．

【解析】

（1）已知条件由正弦定理化边为角后，由两角和的正弦公式和诱导公式求得主，再由余弦定理求得；

（2）由（1）可得的范围，再把应用二倍角公式和两角和的正弦公式化为一个角一个三角函数形式，然后根据正弦函数性质得结论．

（1）∵acosB+bcosA＝2ccosB，

∴根据正弦定理得，sinAcosB+sinBcosA＝2sinCcosB，

∴sin（A+B）＝2sinCcosB，

∴sinC＝2sinCcosB，

∵sinC≠0，

故cosB，

∵a＝3，，

由余弦定理可得，，

∴c＝1或c＝2；

（2）∵

，

＝sin（2A），

由（1）知，B，

∴，

∴，

∴，，

∴的取值范围为．